Ponte al km 0+193 della S.S.
49 bis
La Società 4 EMME Service S.p.A. specializzata
nell’esecuzione di prove sperimentali su strutture in sito, è stata incaricata
di eseguire il monitoraggio dinamico sul ponte al km 0+193 della S.S. 49 bis
per il controllo delle deformazioni-sollecitazioni prodotte dalle vibrazioni
innescate dalle esplosioni durante le fasi di scavo del tunnel pilota del
Brennero.
A questo scopo è stato analizzato il ponte attraverso l’esecuzione di
un modello agli elementi finiti, calibrato sulla base di una serie di risultati
sperimentali.
Dal modello calibrato sono stati calcolati i valori di spostamento
ottenuti sia per effetto sismico sia per il passaggio dei carichi di categoria.
Sulla base dei valori ottenuti sono stati definiti degli spostamenti
massimi, presentati nel Piano Esecutivo di Sicurezza, indicati come valori
limite per il monitoraggio dinamico durante le fasi di volata.
Il viadotto sul fiume Isarco è costruito in c.a. ed è lungo 184,15 m. Lo schema statico è quello di una struttura isostatica, a 4 campate, di cui una, la prima e la più corta, semplicemente appoggiata sulla spalla lato Bressanone e sulla prima pila, mentre le altre tre sono intervallate da due pile che sorreggono due mensole a cavaliere ciascuna, reggenti a loro volta le travate di uguale luce. La struttura portante dell’impalcato è costituita da 3 travi principali e due mensole laterali.

·
luce della I campata: 22,62
m;
·
luce delle tre travate: 40 m;
·
luce mensole a cavaliere: 9,5 m;
·
n° di travi principali: 3
·
larghezza travi principali: 0,70 m;
·
interasse travi principali: 3,30 m;
·
larghezza carreggiata: 7,50 m;
·
larghezza impalcato: 9,60
m.

MODELLAZIONE
NUMERICA CALIBRATA
La
modellazione agli elementi finiti del ponte oggetto della presente analisi, è
realizzata con il codice di analisi strutturale Straus7, release
2.3.6 distribuito dalla società H.S.H. srl di Padova.

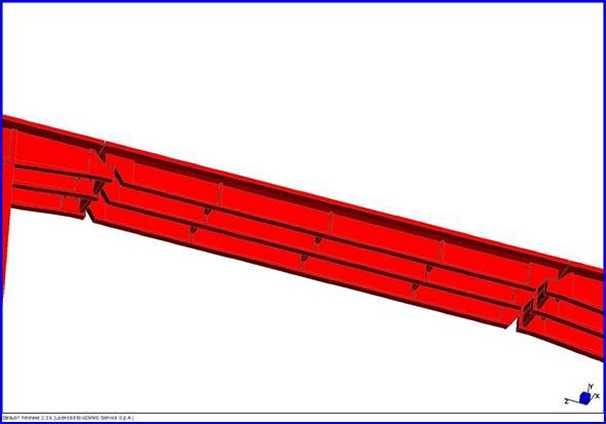
Vista assonometrica dal basso del modello
agli elementi finiti
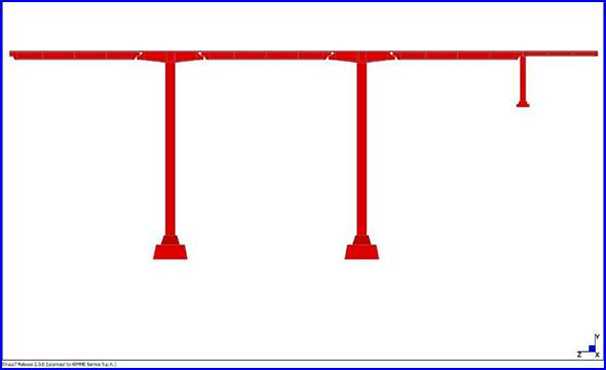
Prospetto
Trave L=
La
modellazione della struttura ha richiesto l’utilizzo di 90.887 nodi e 52.122
elementi solidi. Il modello strutturale viene calibrato tramite la simulazione
delle caratteristiche dinamiche misurate sperimentalmente.
Di
seguito si espongono i principali componenti parametrici di contorno del
modello calibrato.
|
ELEMENTO |
MATERIALE |
N°
ELEMENTI |
E [MPa] |
n |
ρ
[kN/m3] |
|
Pile |
Calcestruzzo |
11.904 |
32.000 |
0,20 |
25,00 |
|
Plinti |
Calcestruzzo |
1.734 |
32.000 |
0,20 |
25,00 |
|
Travi longitudinali |
Calcestruzzo |
23.412 |
35.000 |
0,20 |
25,00 |
|
Traversi |
Calcestruzzo |
3.016 |
35.000 |
0,20 |
25,00 |
|
Soletta |
Calcestruzzo |
12.056 |
35.000 |
0.20 |
25,00 |
Nelle
immagini successive si riportano le viste assonometriche dei principali modi di
vibrare della struttura.
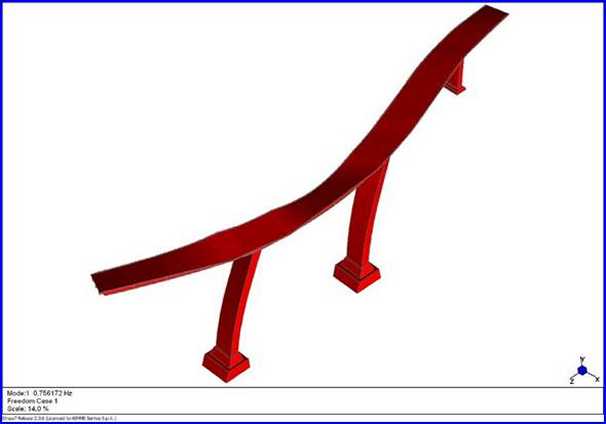
Vista assonometrica del I modo di vibrare, f1 = 0,75 Hz
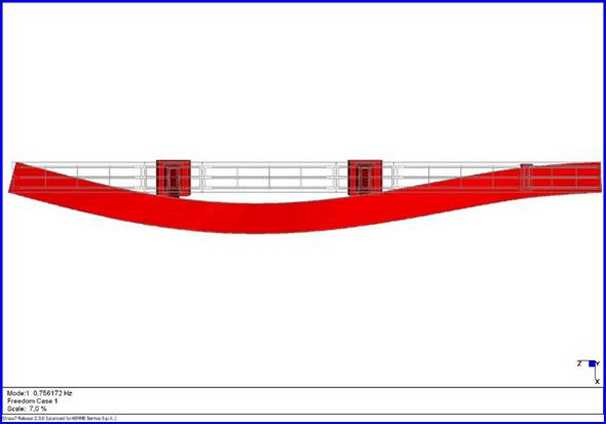
Vista planimetrica del
I modo di vibrare, f1 = 0,75 Hz con sovrapposizione della configurazione
indeformata

Vista assonometrica del II modo di vibrare, f2 = 0,81 Hz

Vista prospettica del
II modo di vibrare, f2 =081 Hz con sovrapposizione
della configurazione indeformata

Vista assonometrica del III modo di vibrare, f3 = 1,68 Hz
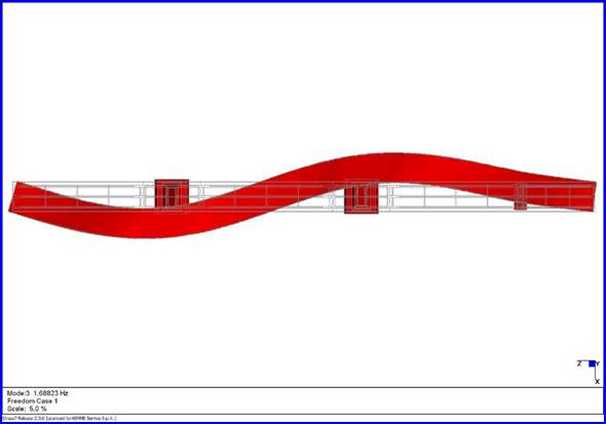
Vista planimetrica del
III modo di vibrare, f3 = 1,68 Hz con sovrapposizione
della configurazione indeformata

Vista assonometrica del IV modo di vibrare, f4 = 2,05 Hz

Vista prospettica del
IV modo di vibrare, f4 = 2,05 Hz con sovrapposizione
della configurazione indeformata

Vista assonometrica del V modo di vibrare, f5 = 2,50 Hz
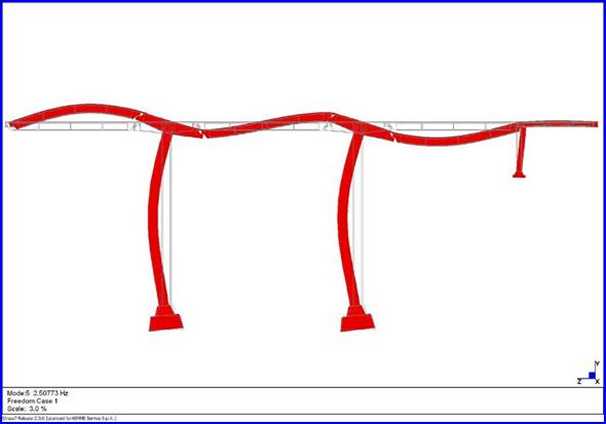
Vista prospettica del
V modo di vibrare, f5 = 2,50 Hz con sovrapposizione
della configurazione indeformata

Vista assonometrica del VI modo di vibrare, f6 = 3,11 Hz

Vista assonometrica del VII modo di vibrare, f7 = 3,46 Hz
Le
frequenze teoriche ottenute sono riportate di seguito.
FREQUENZE DEL MODELLO CALIBRATO
|
DESCRIZIONE |
FREQUENZA
(Hz) |
|
I Modo |
0,75
(trasversale) |
|
II Modo |
0,81
(longitudinale) |
|
III Modo |
1,68
(trasversale) |
|
IV Modo |
2,05
(verticale) |
|
V Modo |
2,50
(verticale) |
|
VI Modo |
3,11
(torsionale) |
|
VII Modo |
3,46
(verticale) |
SIMULAZIONE
DEI FENOMENI INDOTTI DALLE ESPLOSIONI
Per poter valutare le
accelerazioni nei punti più sensibili della struttura indotte dalle esplosioni
è stato simulato il passaggio di spettri di eccitazione sulle fondazioni
corrispondente a quello dovuto ad un’azione sismica.
Gli spettri di
eccitazione comportano delle tensioni nelle direzioni del piano orizzontale
che, se rientranti nella normativa in vigore, vengono assunte, attraverso i
rispettivi spostamenti/accelerazioni, come parametri di confronto.
Per la valutazione
dell’azione sismica è stata eseguita un’analisi dinamica adottando come spettro
di risposta, in termini di accelerazione, la seguente espressione:
![]() con
con ![]()
dove:
C = coefficiente di
intensità sismica
S = grado di sismicità (S=6 bassa sismicità)
I = coefficiente di
protezione sismica
R = coefficiente di risposta
che vale 0,862/T02/3 per T > 0,8 s
1,0 per T ≤ 0,8 s
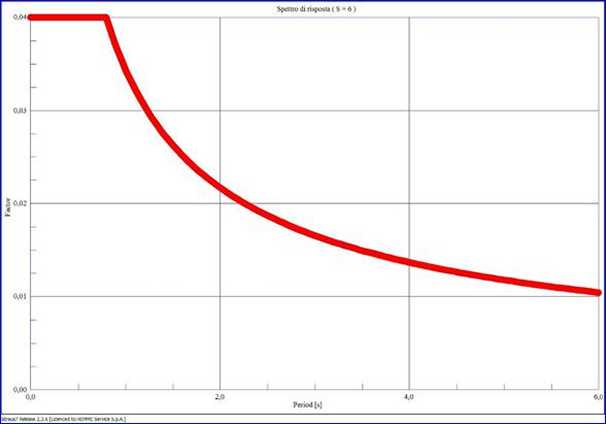
Spettro di risposta
L’analisi modale tiene conto dei primi 30 modi di
vibrazione sufficienti ad assicurare l’eccitazione di più dell’85% della massa
totale della struttura.
Di seguito sono riportati gli spostamenti della
struttura per effetto del sisma in direzione longitudinale , trasversale e
verticale.
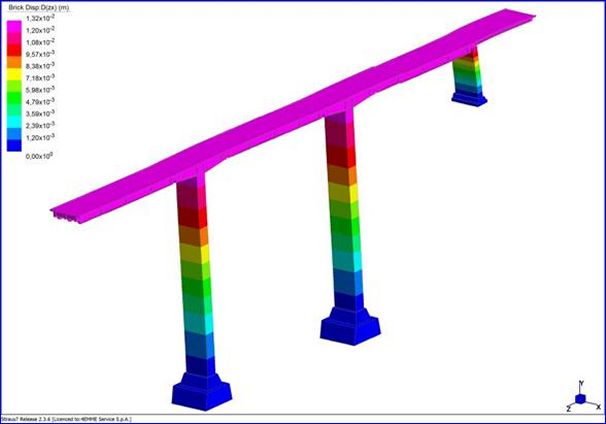
Spostamenti
longitudinali – Sisma in direzione longitudinale
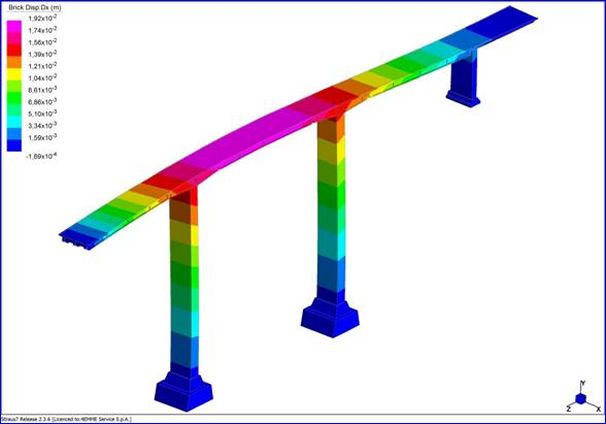
Spostamenti
trasversali – Sisma in direzione trasversale
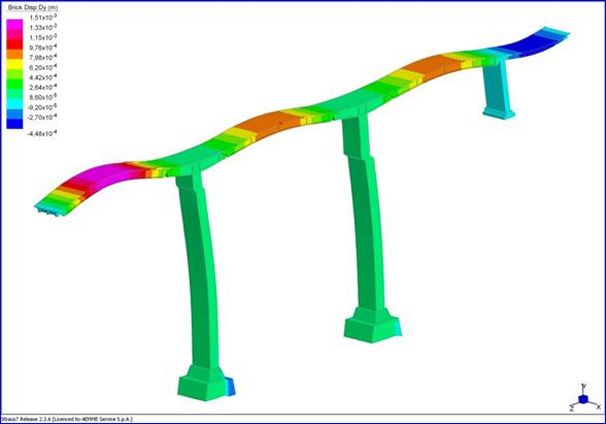
Spostamenti
verticali – Sisma in direzione verticale
Per inviare un messaggio: hsh@iperv.it