Scopo del presente studio è quello di individuare un modello agli elementi finiti che possa rappresentare correttamente il comportamento di un pilastro alto di cemento armato soggetto a presso-flessione deviata, tenendo conto anche degli effetti del secondo ordine, ovvero, l’incremento di sollecitazioni conseguente alla deformazione del pilastro stesso.

Oggetto dello studio è un pilastro, incastrato alla base e libero in sommità, avente una sezione trasversale di 100 cm per 100 cm ed un’altezza pari a 2500 cm. L’armatura viene schematizzata con quattro elementi di 50 cm² di superficie posti in prossimità dei vertici a 10 cm dai bordi.

Si assume un sistema cartesiano (terna di assi destrogira) di riferimento con origine in corrispondenza del baricentro della sezione di base, asse delle z verticale e diretto verso l’alto ed assi x ed y paralleli ai lati della base del pilastro.

Le forze e coppie sono applicate sulla sezione di sommità e valgono:

In una prima fase si esegue il calcolo degli spostamenti e tensioni secondo i metodi classici della scienza delle costruzioni. Questi risultati sono utili per valutare la correttezza dei risultati ottenuti con il metodo agli elementi finiti (risultati ovviamente approssimati) e, quindi, scegliere il modello più idoneo per raggiungere lo scopo prefissato.

Si calcolano innanzi tutto gli spostamenti della sezione di sommità, con riguardo ai soli effetti del primo ordine, nell’ipotesi di sezione completamente reagente. Essi sono:

Si indicano ora gli spostamenti, sempre del primo ordine, calcolati trascurando, come di consueto, il contributo del calcestruzzo teso. Per tale calcolo si è diviso il pilastro in tronchetti aventi un’altezza di un centimetro e considerando, per ciascuno di essi, un grado di parzializzazione costante. Essi valgono:

Spostamenti, deformazioni e tensioni del secondo ordine, calcolati dividendo il pilastro in tronchetti aventi un’altezza di un centimetro valgono.

In questo paragrafo si confrontano i risultati ottenuti assumendo diversi modelli che simulano il comportamento della struttura e variando il numero delle iterazioni di calcolo.

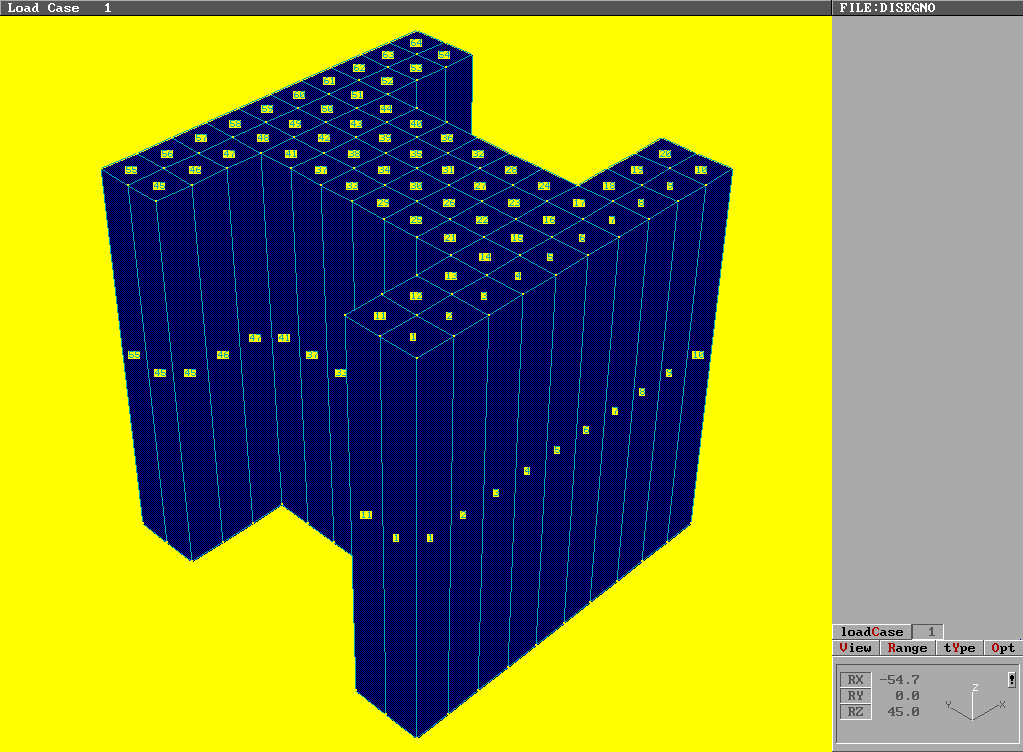
Il pilastro viene diviso in un numero abbastanza limitato di tronchi (in genere sarà sufficiente un numero compreso tra i cinque ed i dieci tronchi); ciascun tronco è diviso inoltre in numero sufficientemente elevato di elementi tridimensionali (brick) ad otto nodi come rappresentato in figura 1.

Fig. 1

Le dimensioni degli elementi brick risultano, generalmente, anomale essendo almeno una dimensione (l’altezza) di almeno un ordine di grandezza maggiore della più piccola dimensione di base.

Nel caso di presso-flessione retta una delle dimensioni della base degli elementi brick potrà essere assunta pari alla larghezza della sezione (in direzione ortogonale al piano di sollecitazione) del pilastro (si veda la figura 2).

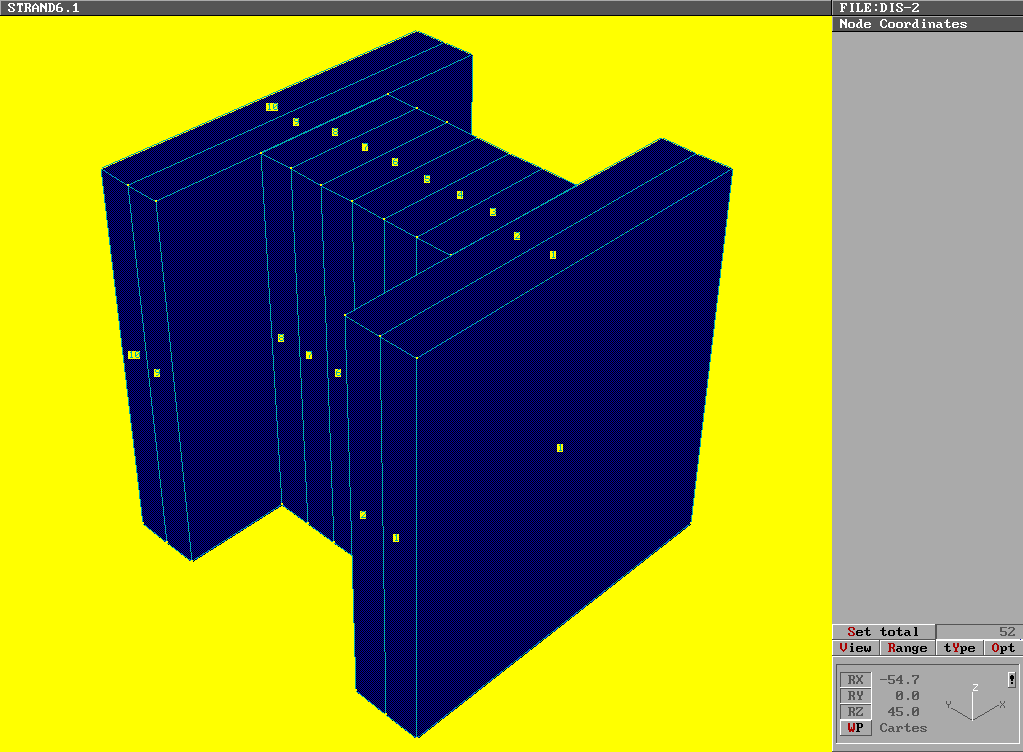Fig. 2

Le armature longitudinali di acciaio si schematizzano come travi prive di rigidezza flessionale e torsionale e saranno disposte lungo gli spigoli verticali degli elementi brick:: ove la posizione delle barre non coincida con gli spigolo degli elementi tridimensionali la barra potrà essere sostituita da due o più barre equivalenti.

Se si vuol garantire il mantenimento delle sezioni piane si inseriranno, in corrispondenza delle divisioni tra i vari tronchi, delle piastre aventi una perfetta deformabilità nel piano (spessore membranale nullo) ed un’infinita rigidezza al di fuori del piano della lastra (spessore flessionale molto elevato). Si ricordi che, dopo la prima iterazione la piastra non giace più nel piano x-y: si dovranno, quindi, bloccare le rotazioni attorno all’asse z.

Il pilastro in oggetto viene analizzato seguendo varie schematizzazioni. I modelli analizzati sono:

1. Divisione in senso verticale in quattro strati aventi le seguenti altezze: 1 m, 3 m, 6 m e 15 m. Ogni tronco è diviso in100 elementi brick aventi le dimensioni di base pari a 10 cm per 10 cm.
2. Modello come il precedente con l’aggiunta di elementi bidimensionali (piastre) in corrispondenza delle sommità dei singoli strati.
3. Divisione in senso verticale in dieci strati di eguale altezza (2.50 m). Ogni tronco è diviso in 100 elementi brick aventi le dimensioni di base pari a 10 cm per 10 cm.
4. Modello come il precedente con l’aggiunta di elementi bidimensionali (piastre) in corrispondenza delle sommità dei singoli strati.
5. Divisione in senso verticale in dieci strati di eguale altezza (2.50 m). Ogni tronco è diviso in 400 elementi brick aventi le dimensioni di base pari a 5 cm per 5 cm.
6. Modello come il precedente con l’aggiunta di elementi bidimensionali (piastre) in corrispondenza delle sommità dei singoli strati.

Per quanto concerne il calcestruzzo, non volendo eseguire un calcolo a rottura, si è assunto:

1. Modulo di elasticità costante pari a 35000 MPa a compressione senza un limite superiore per la contrazione massima.
2. Modulo di elasticità pari a 350 MPa per dilatazioni sino allo 0.001.
3. Modulo di elasticità pari a 3.5 MPa per dilatazioni comprese tra i valori di 0.001 e 0.101.

Tutti i modelli analizzati presentano le seguenti condizioni di vincolo:

• In tutti i nodi di base sono bloccati gli spostamenti verticali (paralleli all’asse z).
• La base dell’asse del pilastro è bloccata rispetto a tutti gli spostamenti e rotazioni.
• L’asse mediano di una faccia del pilastro parallela al piano x-z è bloccata, alla base, anche rispetto agli spostamenti in direzione dell’asse x.
• Gli spostamenti sono indicati in centimetri e le tensioni in mega-Pascal.

Tali spostamenti vengono calcolati per valutare l’attendibilità del modello per geometria (spostamenti a sezione tutta reagente) e per schematizzazione del materiale (spostamenti a sezione parzializzata).

I risultati sono raggruppati nella sottostante tabella:

Gli spostamenti del secondo ordine in sommità (con sezione del pilastro parzializzata) e le tensione nel vertice (calcestruzzo) e nella barra più sollecitati valgono:

Dall’analisi dei risultati riportati nel paragrafo precedente si può osservare come, con esclusione delle tensioni nell’acciaio, i valori più precisi si ottengono dai modelli privi delle piastre che garantiscono il mantenimento delle sezioni piane.

Per i rimanenti modelli si vede che i risultati sono già abbastanza precisi anche con una schematizzazione a soli quattro strati, mentre è praticamente ininfluente la suddivisione in 400 elementi per strato rispetto alla più semplice suddivisione in 100.

Le differenze percentuali, rispetto ai valori ottenuti con i metodi classici della scienza delle costruzioni, sono riportati nella tabella seguente:

Si può osservare che il modello (tipo 1) a quattro strati può essere sufficiente per un primo dimensionamento e verifica del pilastro, mentre il più conveniente per una verifica più precisa è quello corrispondente al modello tipo 2 che richiede tempi di elaborazione molto più limitati, pari a circa un settantesimo, del modello più preciso tipo 3.

Una valutazione più precisa della tensione nell’acciaio si può ricavare analiticamente considerando la posizione dell’asse neutro a partire dalla tensione nel calcestruzzo.

La deformazione del pilastro e le tensioni alla base sono rappresentate nelle sottostanti figure 3 e 4.

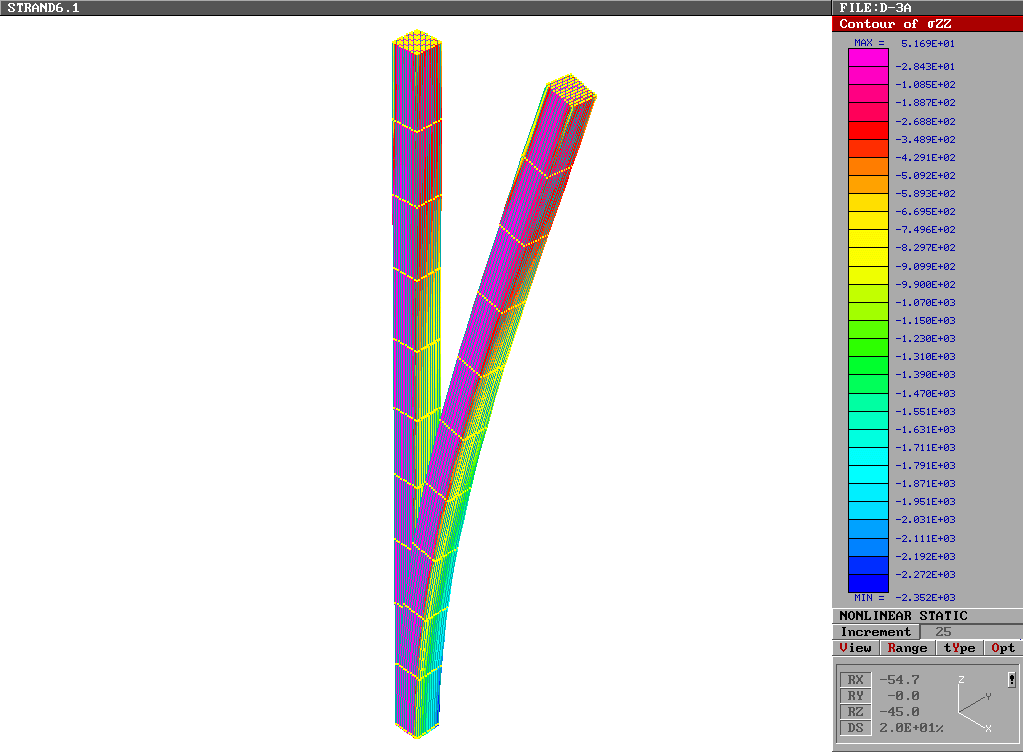
Fig. 3

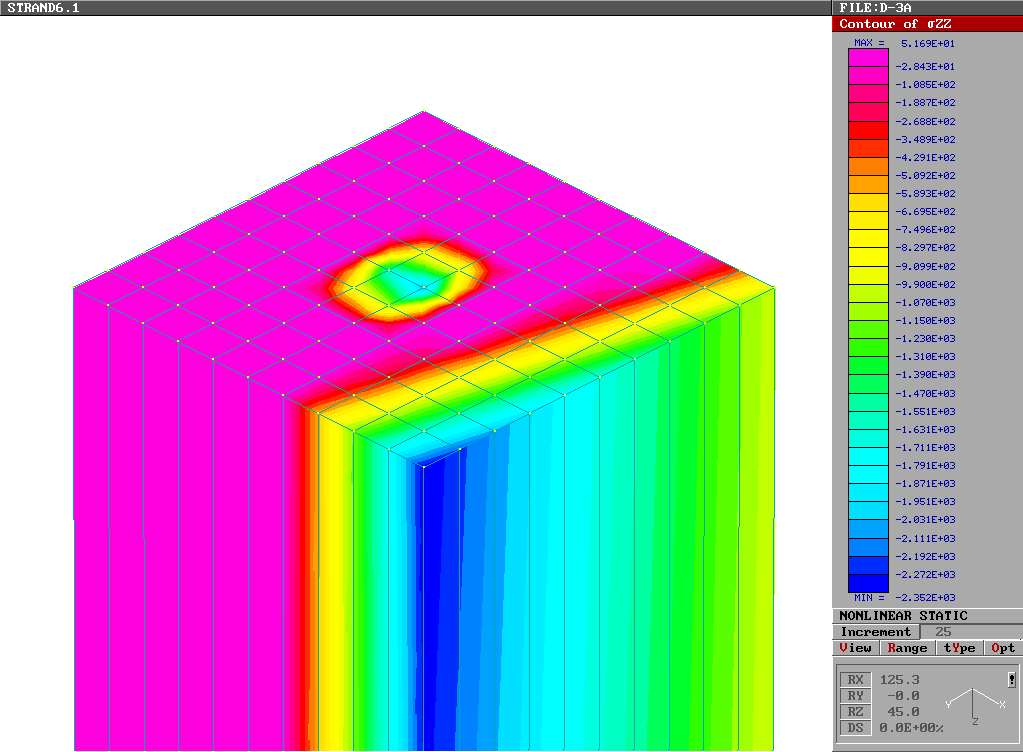
Fig. 4

L’anomalia dell’andamento delle tensioni nella zona centrale del pilastro è dovuta al fatto che il nodo al centro della base è vincolato nelle tre direzioni e, quindi, in questo punto agiscono, come forze concentrate, le reazioni orizzontali (dovute alle forze orizzontali applicate).

Per valutare la convergenza del metodo proposto per l’analisi dello stato di deformazione del sistema si riportano nella seguente tabella i risultati ottenuti con un numero di iterazioni crescente.

Come si può osservare già dopo la sesta iterazione l’errore non è superiore all’1% (circa 2mm per lo spostamento maggiore ed 1 mm per quello minore). Tale errore comporta un variazione nei momenti del secondo ordine.

Per valutare correttamente il significato dei suddetti errori si riportano i momenti massimi che si hanno alla base del pilastro: