Scopo del presente studio è quello di individuare un modello agli elementi finiti che possa rappresentare correttamente il comportamento di una trave snella di cemento armato soggetta a torsione e flessione deviata, tenendo conto anche degli effetti del secondo ordine, ovvero, l’incremento di sollecitazione conseguente alla deformazione della trave stessa.

Risulta pertanto necessario eseguire un’analisi non lineare per geometria (effetti del secondo ordine) e per materiale (calcestruzzo non resistente a trazione e/o diagramma s - e non lineare). Gli elementi finiti utilizzati saranno pertanto elementi tridimensionali brick: in particolare sceglieremo elementi ad otto nodi.

Se si limita l’analisi al comportamento di travi costituite da materiale con diagramma s-e lineare senza limiti superiore ed inferiore per le tensioni in alcuni casi si potrà eseguire il calcolo adottando elementi beam.

1. Materiale "Lineare".

Si analizza , in questo paragrafo, il comportamento di travi costituite da un materiale a resistenza illimitata con diagramma s-e lineare.

In un primo tempo, per valutare la validità della modellazione delle strutture adottata, si calcoleranno i carichi critici delle travi considerate e si confronteranno, ove possibile, con i valori teorici.

Come criterio di giudizio sulla validità degli schemi adottati si confronteranno non tanto le deformazioni del secondo ordine calcolate, ma i valori dei carichi critici. Tali carichi vengono individuati dal punto in cui la deformazione aumenta molto rapidamente all’aumentare del carico.

Si prenda in esame una trave a sezione rettangolare avente le seguenti caratteristiche.

• Sezione 100 mm x 1200 mm;
• Luce pari a 20000 mm;
• Materiale E = 30000 MPa, G = 12500 MPa;
• Carico uniformemente distribuito applicato sull’asse baricentrico (coincidente con l’asse del centro di taglio).

Il calcolo teorico fornisce, per la trave semplicemente appoggiata agli estremi con incastri torsionali, un carico critico:

Per l’analisi mediante il calcolo agli elementi finiti prendiamo in esame diverse schematizzazioni che illustreremo nei paragrafi successivi.

1. Schematizzazione con elementi a trave.

La trave viene divisa in 400 tronchi aventi una lunghezza di 50 mm ed il carico viene considerato applicato sui nodi: Per ottenere lo sbandamento viene applicato, in corrispondenza della sezione di mezzeria, un momento torcente avente un valore piccolo pari a 100 mmN che ha la sola funzione di innescare lo sbandamento della trave.

L’analisi fornisce il seguente carico critico:

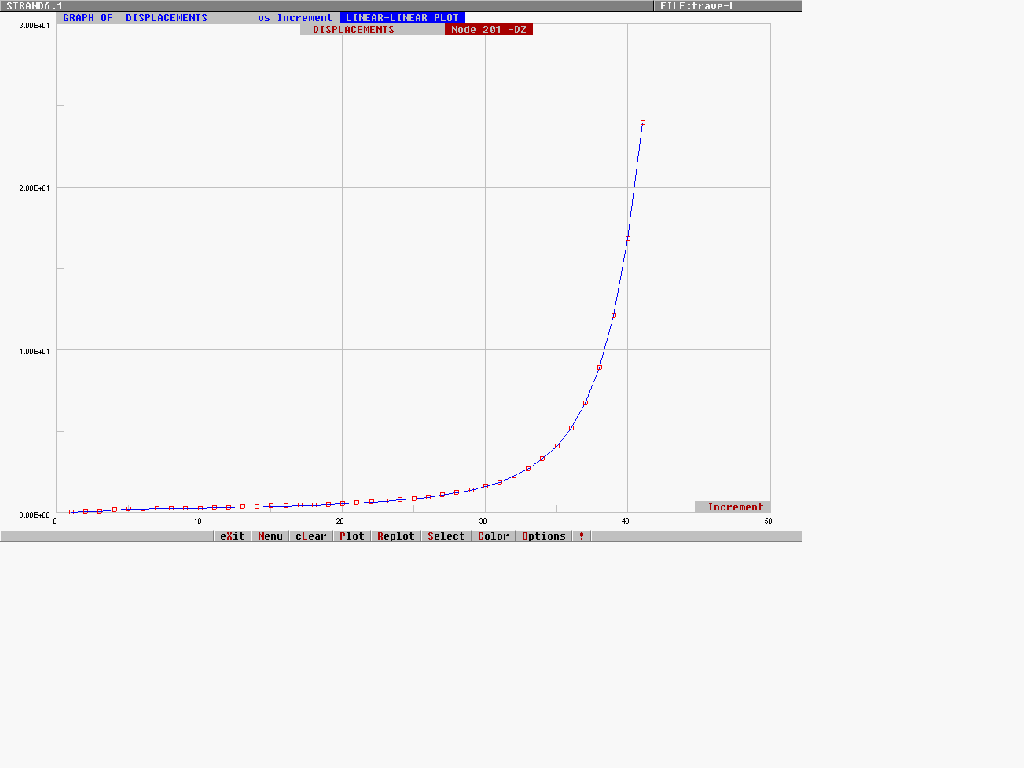
Nella figura n° 1 è rappresentato l’andamento dello spostamento orizzontale (in direzione dell’asse z) della sezione di mezzeria per un carico variabile da 13,100 a 13.500 N/mm.

Fig. 1 – Spostamento trasversale.

Variando il numero di tronchi in cui si divide la trave si ottengono i seguenti valori del carico critico:

• N° 40 tronchi qcr = 13,45 N/mm
• N° 10 tronchi qcr = 13,90 N/mm.

Se i carichi non agiscono nel centro di taglio della sezione non è sufficiente, nello studio delle deformazioni del secondo ordine, applicare tali carichi nel centro di taglio stesso (che, in questo caso particolare, coincide con il baricentro) accompagnati dal momento (torcente) calcolato rispetto a tale punto in quanto, in seguito alle deformazioni non trascurabili della trave, l’eccentricità può variare: si veda, ad esempio, il caso di un carico applicato sull’asse di simmetria verticale della sezione in un punto diverso dal centro di taglio che, in seguito ad una rotazione della sezione, si sposta lateralmente generando un momento torcente.

In questi casi la trave dovrà essere dotata di appendici (travi ad elevata rigidezza flessionale) uscenti dai nodi (corrispondenti alla mesh) e con l’estremità libera in corrispondenza del punto di applicazione del carico.

1. Schematizzazione con elementi brick.

Non sempre è possibile schematizzare la struttura come una trave (sia pure dotandola di appendici per l’applicazione dei carichi), ma, molto spesso, è necessario utilizzare un modello diverso ed, in particolare, una modellazione con elementi brick.

I principali casi in cui la modellazione a trave non è più sufficiente a rappresentare correttamente il funzionamento della struttura sono:

• I vincoli nei punti in cui è appoggiata la trave non sono sufficienti a garantire l’indeformabilità della sezione e pertanto permettono degli spostamenti (in genere orizzontali) dell’asse verticale della sezione stessa.
• La forma della sezione trasversale è dispersa (le più comuni sono, ad esempio, sezioni a C oppure a doppio T) sezioni per le quali non è più valida la teoria di De Saint Venant.
• Il comportamento del materiale non è lineare: modulo di elasticità variabili e/o materiale non resistente a torsione.

è pertanto opportuno valutare il grado di discretizzazione della trave necessario ad ottenere l’approssimazione desiderata. A questo scopo verranno confrontati i risultati (corrispondenti al carico critico uniformemente distribuito applicato sull’asse baricentrico) del modello ad elementi (brick) di varie dimensioni con quelli corrispondenti al calcolo teorico per la trave a sezione rettangolare sottile.

Le dimensioni prescelte ed i risultati sono i seguenti (vista la simmetria si opera su mezza struttura):

1. Le dimensioni degli elementi brick (tutti eguali) sono le seguenti:

• Larghezza = 25 mm;
• Altezza = 75 mm;
• Lunghezza = 200 mm.
• Complessivi 4335 nodi e 3200 bricks.

Il carico critico vale qcr = 13,57 N/mm

1. Le dimensioni degli elementi brick (tutti eguali) sono le seguenti:

• Larghezza = 25 mm;
• Altezza = 75 mm;
• Lunghezza = 400 mm.
• Complessivi 2210 nodi e 1600 bricks.

Il carico critico vale qcr = 13,59 N/mm

1. Le dimensioni degli elementi brick (tutti eguali) sono le seguenti:

• Larghezza = 25 mm;
• Altezza = 75 mm;
• Lunghezza =1000 mm.
• Complessivi 935 nodi e 640 bricks.

Il carico critico vale qcr = 13,66 N/mm

1. Le dimensioni degli elementi brick (tutti eguali) sono le seguenti:

• Larghezza = 25 mm;
• Altezza = 75 mm;
• Lunghezza =2000 mm.
• Complessivi 510 nodi e 800 bricks.

Il carico critico vale qcr = 13,81 N/mm

1. Le dimensioni degli elementi brick (tutti eguali) sono le seguenti:

• Larghezza = 50 mm;
• Altezza = 100 mm;
• Lunghezza = 200 mm.
• Complessivi 1989 nodi e 1200 bricks.

Il carico critico vale qcr = 10,81 N/mm

Si può notare che, almeno in questo caso, la lunghezza dei tronchi non ha una sensibile influenza sull’approssimazione dei risultati: una variazione di lunghezza da 200 a 2000 mm porta una variazione del carico critico calcolato inferiore al 2%.

Una notevole variazione del carico critico calcolato si ha, invece, con l’aumento delle dimensioni trasversali degli elementi brick

Si prende in esame una trave con sezione a doppio T avente le seguenti caratteristiche.

• Altezza complessiva pari a 1800 mm;
• Spessore dell’anima di 120 mm;
• Ala superiore con larghezza di 1220 mm e spessore variabile da 100 a 140 mm;
• Ala inferiore con larghezza di 920 mm e spessore variabile da 80 a 100 mm;
• Luce pari a 30000 mm;
• Materiale E = 30000 Mpa, G = 12500 Mpa;
• Carico uniformemente distribuito applicato nella mezzeria dell’ala superiore.

Il calcolo teorico fornisce, per la trave semplicemente appoggiata agli estremi con incastri torsionali, un carico critico:

Nella determinazione di questo carico hanno influenza due parametri:

coefficiente questo che tiene conto della sezione a doppio T. Questo coefficiente, come vedremo ne paragrafo seguente, è largamente sottostimato in quanto deriva dall’ipotesi di sezione composta da lastre sottili.

coefficiente, quest’ultimo, che tiene conto della posizione del carico.

Per l’analisi mediante il calcolo agli elementi finiti prendiamo in esame diverse schematizzazioni che illustreremo nei paragrafi successivi.

1. Schematizzazione con elementi trave.

Nel caso di sezioni a doppio T simmetriche rispetto al piano medio dell’anima la trave stessa può essere assimilata ad un sistema piano di travi costituito da tre aste longitudinali (rappresentanti l’ala superiore, l’anima e l’ala inferiore) collegate da aste verticali di opportuna rigidezza in numero variabile a seconda della precisione di calcolo che si vuol raggiungere.

Considerando una trave con asse longitudinale orizzontale e piano medio dell’anima verticale scegliamo come sistema di riferimento una terna di assi cartesiana con asse Y verticale, asse X parallelo all’asse della trave ed asse Z trasversale.

Le tre travi longitudinali avranno le seguenti caratteristiche:

• Asse longitudinale coincidente con l’asse baricentrico rispettivamente dell’ala superiore, dell’anima e dell’ala inferiore.
• Caratteristiche di rigidezza flessionale e torsionale eguali a quelle delle parti di trave sopra definite e supposte isolate.

Per le travi verticali "di collegamento" si adotterà una rigidezza flessionale molto elevata nel piano x-y e corrispondente a quello dell’anima, moltiplicato per l’interasse tra le suddette travi, al di fuori del piano dell’anima stessa.

Nel caso preso in esame come esempio si è supposta rigidezza infinita in entrambe le direzioni: tale assunzione corrisponde all’ipotesi di sezione indeformabile nel suo piano.

I risultati (carico critico) ottenuti, per le varie schematizzazioni (numero dei collegamenti trasversali) sono i seguenti:

• n° 300 traversi (D x = 50 mm) -> qcr = 146,9 N/mm.
• n° 150 traversi (D x = 100 mm) -> qcr = 145,4 N/mm.
• n° 30 traversi (D x = 500 mm) -> qcr = 129,9 N/mm.
• n° 15 traversi (D x = 1000 mm) -> qcr = 111,9 N/mm.

Confrontando i risultati ottenuti con varie mesh (non riportati in questa sede) si vede che la suddivisione che dà i migliori risultati (intesi come rapporto precisione / tempo di elaborazione) è quella corrispondente ad una divisione in tronchi aventi una lunghezza di 1000 mm e dimensioni trasversali pari a 40 mm x 120 mm per l’anima e suddivisione in due strati costituiti da 13 elementi ciascuno per l’ala inferire e tre strati con 15 brick per strato nell’ala superiore.

Complessivamente si hanno 2464 nodi e 1650 elementi.

Il carico iniziale, sul quale si applicano gli incrementi sino ad arrivare al carico critico, è costituito da un carico pari a 50000 N per ogni sezione trasversale (poste ad una distanza di 1,0 m) ed un momento torcente in mezzeria (momento che serve per innescare lo sbandamento) di 1,6 kNm

Come si vede dalle seguenti figure 2 e 3 non c’è un punto ben definito in cui gli spostamenti aumentino improvvisamente (corrispondente al carico critico), ma l’aumento è abbastanza progressivo . Il carico critico verrà, allora, fissato convenzionalmente in funzione di uno spostamento predefinito: in particolare si potrà dire di aver raggiunto tale carico quando la freccia raggiunge, ad esempio, un trecentesimo della luce ovvero 100mm.

Tale freccia laterale è raggiunta al sedicesimo incremento (104,4 mm) corrispondente ad un carico critico pari a:

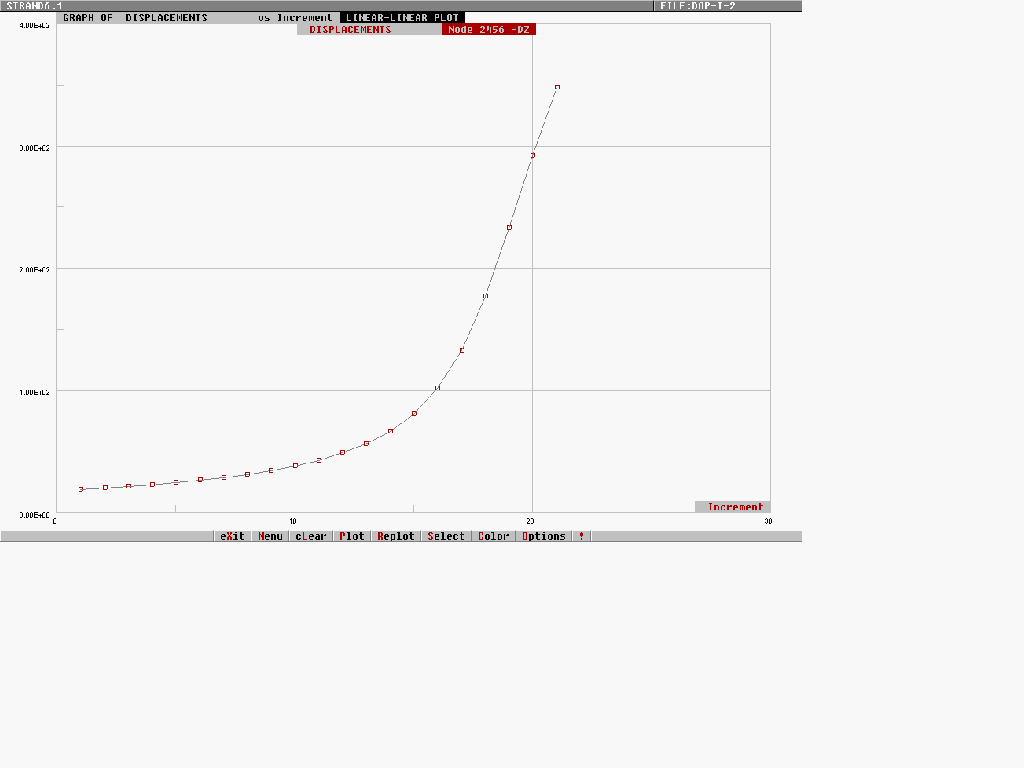
Fig. 2 – Spostamento trasversale.

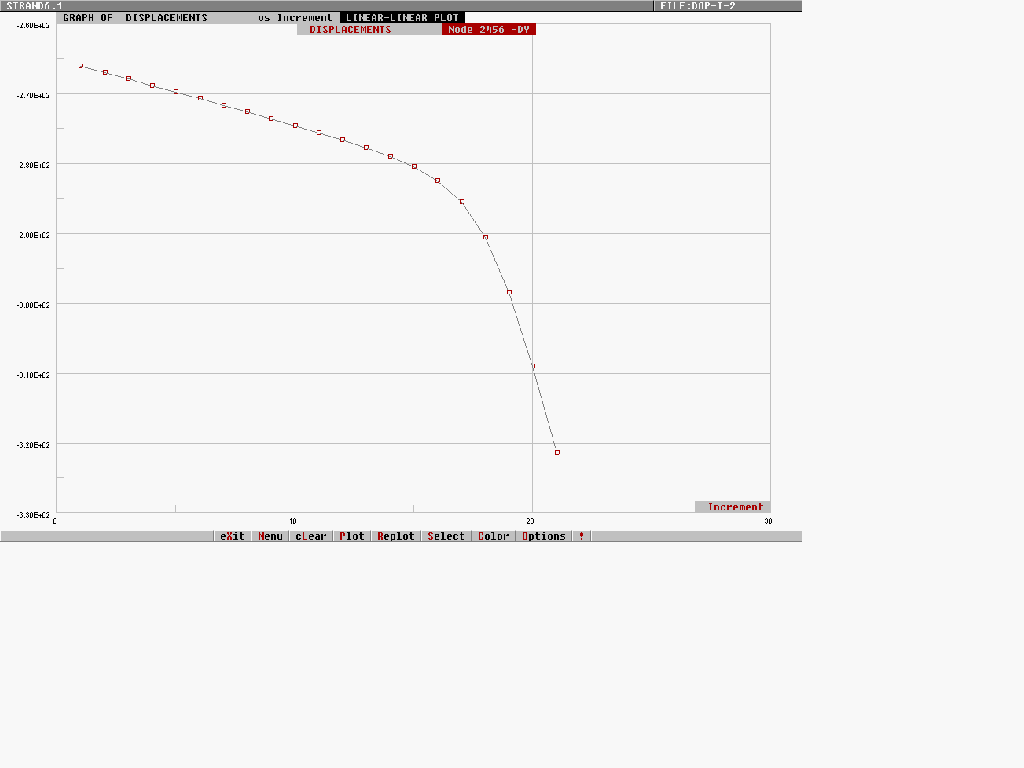
Fig. 3 – Spostamento verticale.

Se il carico viene applicato in corrispondenza del centro di taglio (a 486,9 mm dal bordo superiore) il carico critico vale 171,0 N/mm, con uno spostamento laterale di 106,0 mm.

In conclusione, con materiale a comportamento lineare, si può affermare quanto segue:

• Il carico critico calcolato con il metodo degli elementi finiti (elemento tridimensionali) è nettamente superiore a quello valutato con i metodi tradizionali: l’incremento è pari al 10%.
• La variazione di carico dovuta al punto di applicazione del carico (coefficiente k1) è eguale all’ 11,2 % quando si esegue il calcolo con i metodi tradizionale e 12% con il metodo degli elementi finiti.

1. Materiale " Non Lineare".

Si analizza ora una trave avente le stesse dimensioni di quella vista al paragrafo 1.1. precompressa mediante cavi rettilinei disposti a 40 mm dal bordo inferiore, aventi un’area di 350 mm2 e posta a 40 mm dal bordo superiore con una superficie di 140 mm2. Tutti i cavi sono soggetti ad una pretensione con tensione di 1140 MPa.

Il carico verticale (unico carico applicato) è uniformemente distribuito sulla parte superiore e presenta un’eccentricità trasversale di 10 mm.

Si vuole valutare l’influenza della non linearità del diagramma s-e del calcestruzzo. Si confrontano i risultati ottenuti nelle tre seguenti ipotesi:

1. Modulo di elasticità costante : E = 30000 MPa.
2. Modulo di elasticità pari a 30000 MPa in compressione e 20000 MPa in trazione; criterio delle massime tensioni.
3. Modulo di elasticità variabile da 500 Mpa a 10000 MPa in trazione e da 30000Mpa a 2000 Mpa in compressione (si veda la sottostante fig. 4).

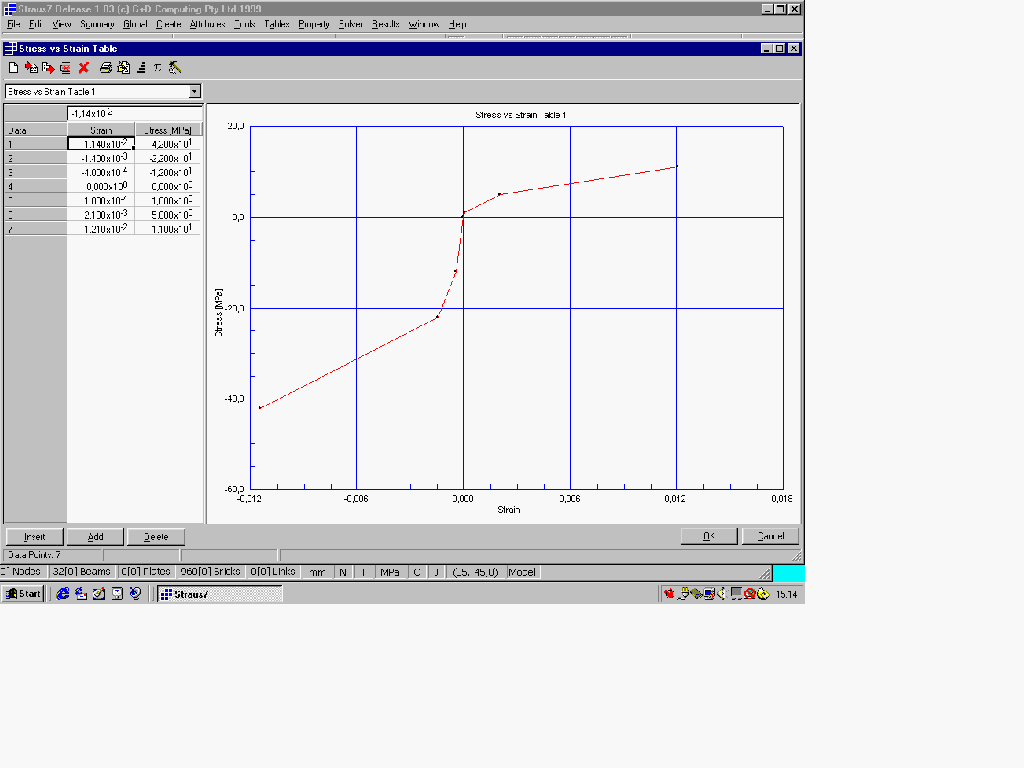
Fig. 4 - Diagramma s-e del calcestruzzo.

Per un’accurata analisi della tensioni si sceglie una mesh più sottile per la sezione trasversale in quanto, in queste sezioni, la variazione delle tensioni (e di conseguenza quella dei moduli di elasticità) è più rapida. Per quanto concerne le dimensioni longitudinali si è visto, nel caso analizzato al paragrafo 1.1., non hanno una grande influenza. Si sceglieranno, pertanto, elementi selle dimensioni di 40 x 40 x 1250 mm.

Le tensioni che verranno di seguito riportate sono quelle che si verificano nella sezione di mezzeria al bordo inferiore e superiore in corrispondenza dell’asse di simmetria della sezione. Verranno inoltre riportate le tensioni nelle barre di acciaio preteso ( si fa riferimento alle barre rispettivamente inferiori e superiori).

Criterio di calc.	Beton si	Beton ss	Acciaio Arm. si	Acciaio Arm. ss
1	-18,17	+0,66	+1031	+1141
2	-18,18	+0,44	+1031	+1141
3	-15,29	+0,56	+1007	+1151

Il carico critico, valutato secondo l’ipotesi n° 3 (modulo si elasticità variabile), vale:

Le tensioni nel calcestruzzo bordo inferiore e superiore:

e nell’acciaio armonico:

si = +944 MPa e ss = +1126 MPa