DOCUMENTAZIONE TECNICA
CODICE DI CALCOLO STRAUS
ESEMPIO DI CALCOLAZIONE TIPO
Calcolo dell’armatura per le mensole tozze
-CALCOLO ELASTICO ED A ROTTURA-
Prof. Antonio CASELLATO
Universita' di Padova
OGGETTO.
La presente nota si propone di indicare un procedimento rapido e sufficientemente preciso per il calcolo e la verifica di una mensola tozza di calcestruzzo di cemento armato.
Trattasi di una mensola su pilastro 500x500 mm.
Dimensioni della mensola: Sbalzo 500 mm
Altezza 400-900 mm
Altezza del tronco di pilastro al di sotto della mensola (incastrato alla base): 900 mm;
Altezza del tronco di pilastro al di sopra della mensola (semplicemente appoggiato in sommità in direzione orizzontale): 900 mm.
Si considerano le seguenti condizioni di carico:
- condizione di carico 1: sulla mensola P = 240 kN verticali distribuiti sulla superficie superiore della mensola da 250 a 450 mm; con un carico orizzontale pari a 24 kN orizzontali;
- condizione di carico 2: come sopra ma distribuito anche sull’altezza della mensola
- condizione di carico 3: sforzo normale distribuito in sommità del pilastro di 500 kN.
Sono inoltre previste le seguenti combinazioni di carico:
- prima combinazione: sforzo normale nel pilastro e carico sulla superficie superiore della mensola.
- seconda combinazione: sforzo normale nel pilastro e carico distribuito anche sull’altezza della mensola.
- SCELTA MODELLO.
Si fa riferimento ad un sistema di assi cartesiani:
asse x: orizzontale parallelo all’asse della trave e diretto dall’incastro verso la mensola,
asse y: verticale diretto verso l’alto.
Per quanto concerne la struttura di calcestruzzo si scelgono due modelli:
- MODELLO A LASTRA.
Visto il tipo di sollecitazione la struttura viene schematizzata come un sistema piano (di deformazione) costituita da elementi di lastra quadrati (nella parte inferiore della mensola triangolari) con lato di 50 mm e spessore pari a 500 mm (vedi fig. 1) con complessivi 1136 nodi e 1035 elementi lastra.

Fig. 1 – Schema della mensola e relativa mesh.
- MODELLO A GRATICCIO DI TRAVI.
Scopo di questa schematizzazione è quello di ridurre i tempi di elaborazione (nell’analisi non lineare con materiale non resistente a trazione) senza peraltro ridurre in maniera significativa la precisione di calcolo.
Lo schema dell’elemento corrisponde ad un sistema di 6 travi (due diagonali e quattro lungo i lati) privi di rigidezza flessionale.
Si assume per le travi diagonali un’area di 23000 mm2 e per quelle longitudinali e trasversali pari a 7500 mm2. Spost. dx
Nella tabella seguente sono confrontati, per le varie condizioni elementari di calcolo, gli spostamenti dell’estremità libera della mensola calcolati con la schematizzazione a graticcio (proposta) e quella a lastra: gli spostamenti sono indicati in millimetri
|
Condizione di carico |
Schema a GRATICCIO |
Schema a LASTRA |
|
Spost. dx |
Spost. dy |
Spost. dx |
Spost. dy |
|
c.c. n° 1 |
0,327 |
-0,262 |
0,321 |
-0,267 |
|
c.c. n° 2 |
0,314 |
-0,247 |
0,313 |
-0,254 |
|
c.c. n° 3 |
0,050 |
-0,136 |
0,035 |
-0,125 |
con errori, in particolare per i casi di carico diretto sulla mensola, molto piccoli.
ANALISI DELLE TENSIONI.
I risultati dell’analisi delle tensioni , per la struttura di solo calcestruzzo resistente anche a trazione, sono riportati nelle figure qui di seguito per la prima e seconda combinazione di carico.

Fig. 2 – Carichi concentrati: Tensioni principali.

Fig. 3 – Carichi distribuiti: Tensioni principali.

Fig. 4 - Tensioni principali di trazione su di una sezione verticale a 5 cm dall’attacco della mensola:
azzurro -> carichi concentrati, rosso -> carichi distribuiti
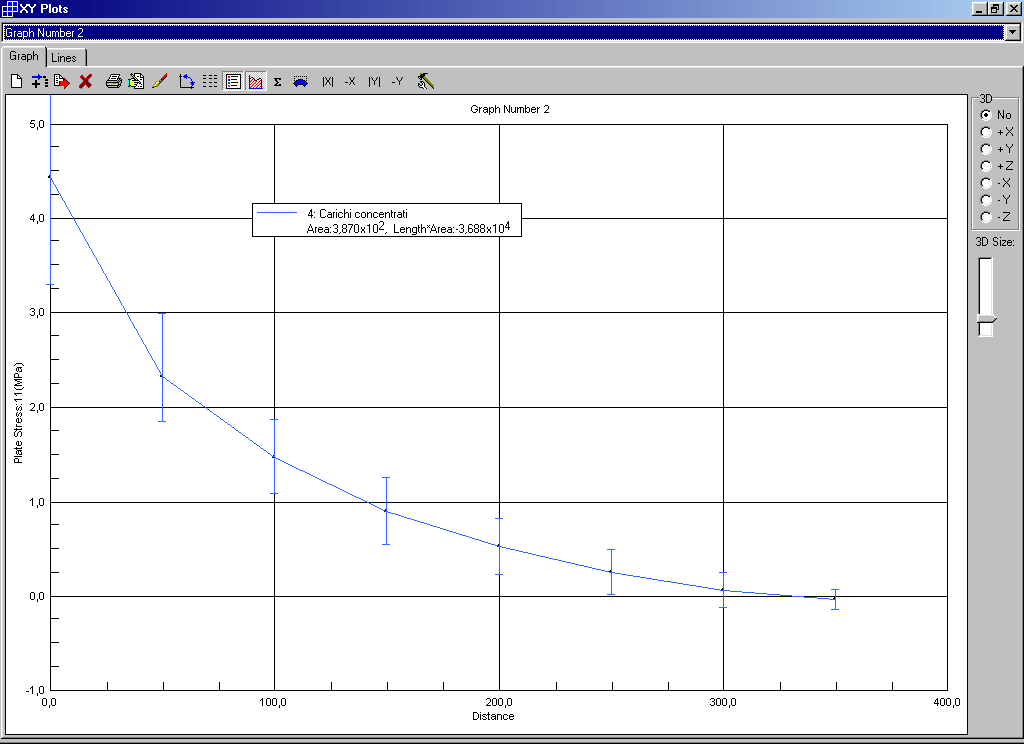
Fig. 5 - Dettaglio grafico precedente (soli carichi concentrati) per la parte di trazione.
Dai grafici qui sopra riportati si nota che lo stato di tensione non varia sensibilmente dalle condizioni di carico concentrato superiormente a quella di carico distribuito sull’altezza della mensola.
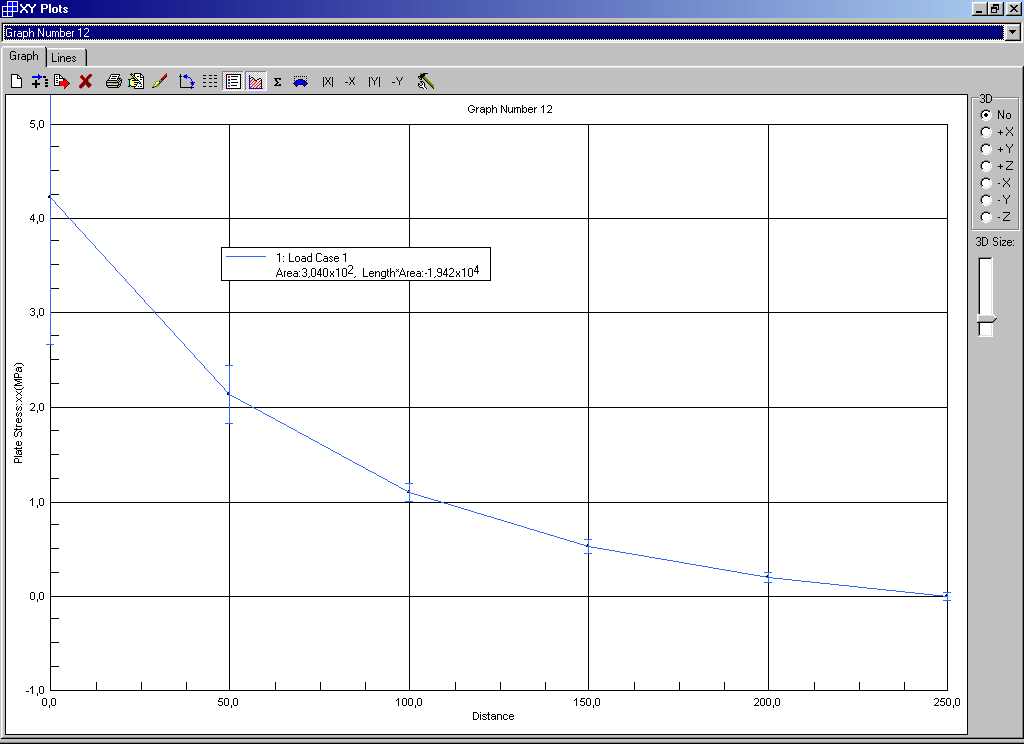
Fig. 6 – Tensioni in direzione x (di trazione) a 5 cm dall’attacco della mensola.
CALCOLO DELL’ARMATURA.
L’armatura viene calcolata dapprima secondo i metodi tradizionali ed, in un secondo momento, utilizzando il procedimento di calcolo agli elementi finiti col metodo che verrà qui di seguito proposto.
L’armatura viene dimensionata considerando una tensione ammissibile pari a 240 MPa.
3.1. METODO TRADIZIONALE.
Armatura orizzontale superiore
Aa=(P*a/(0,85*ho)+H)/sa
=(240000*350/(0,85*850)+24000)/240
=584,43 mm2
armatura obliqua
Ao= 0,25* Aa
= 0,25*584,43
= 146,11 mm2
staffe orizzontali (in alternativa all’armatura obliqua)
As = Ao
= 146,11 mm2
3.2. METODO PROPOSTO.
Armatura orizzontale superiore:
L’armatura orizzontale superiore è posta a 25 mm dalla superficie della mensola..Dal diagramma di fig. 5 integrando gli sforzi relativi ai 50 mm superiori si ottiene uno sforzo di trazione:
Z = (4,434 + 2,327)/2 * 50 * 500
= 84500 N
che risulta inclinato (vedi fig. 2) di circa 45°: la componente orizzontale vale allora approssimativamente:
Z’ = 60000 N
In alternativa lo sforzo di trazione può essere valutato (vedi diagramma di fig. 6) integrando le tensioni sx nello stesso intervallo. Si ha allora:
Z’ = 79500 N
Si disporranno allora 2 barre da 14 mm di diametro.
Staffe orizzontali
Dal diagramma di fig. 2 integrando le tensioni principali di trazione per i successivi 30 cm (ovvero per tutta la restante zona tesa) si ha:
Z = (387,0 – 169,0)*500
=109000 N ( distribuiti da 50 mm a 350 mm )
Essendo la tensione principale inclinata approssimativamente a 45° la componente orizzontale dello sforzo di trazione vale allora:
Z’ = 12800 N ogni 50 mm (valore medio);
In alternativa si può far riferimento al diagramma di fig. 6 (tensioni sx ) integrando per l’intera zona tesa (200 mm) ottenendo:
Z’ = 17000 N ogni 50 mm (valore medio)
Si dispongono staffe a due bracci da 6 mm di diametro.
Staffe del pilastro:
Nella zona interessata dalla mensola si dispongono, nel pilastro, staffe a due bracci aventi un diametro di 8 mm ad un interasse di 10 cm.
Armatura ordinaria del pilastro:
Si prevede un’armatura ordinaria costituita da 4 barre da 26 mm di diametro e quattro da 20 mm.
Nella zona della mensola si dispongono, inoltre, due barre da 20 mm dalla parte della mensola.
VERIFICA DELL’ARMATURA.
Nel presente paragrafo si verificheranno le tensioni nell’armatura e si procederà all’eventuale correzione del suo dimensionamento.
Per tale calcolo si farà riferimento al modello a graticcio con travi prive di rigidezza torsionale, come definito al punto 1.2., rappresentanti la struttura di calcestruzzo cui si sovrappone un graticcio di travi (pure prive di rigidezza flessionale) rappresentanti l’armatura di acciaio.
- VERIFICA PRIMO DIMENSIONAMENTO.
Il calcolo delle tensioni viene qui eseguito considerando le barre di acciaio aventi resistenza illimitata e comportamento lineare del materiale e il calcestruzzo resistente a compressione con la limitazione di tensione convenzionale (riferita alla barre de reticolo) pari a 50 MPa ed a trazione di 0,5 MPa.
Armatura superiore della trave:
La tensione massima rilevata vale: s = 270 MPa.
L’armatura verrà pertanto modificata aumentando il diametro delle barre a 16 mm.
Staffe orizzontali della mensola:
La tensione massima rilevata vale: s = 290 MPa.
L’armatura verrà pertanto modificata aumentando il diametro delle barre a 7 mm.
Per le restanti armature la tensione rimane largamente inferiore al limite di 240 MPa. Non Si ritiene opportuno di ridurre l’armatura.
- VERIFICA SECONDO DIMENSIONAMENTO.
Con l’introduzione delle nuove armature le tensioni rimangono nei limiti prestabiliti (205 MPa per l’armatura superiore e 215 MPa per le staffe orizzontali) e pertanto questa sarà ritenuta l’armatura definitiva.
- VERIFICA FINALE
Se le correzioni apportate sono, come in questo caso, modeste si può passare alla verifica più avanzata mirante al calcolo del coefficiente di sicurezza a rottura (comportante ovviamente tempi di elaborazione maggiorati) in cui si considereranno tutte le barre aventi un comportamento lineare sino alla tensione di snervamento di 540 MPa e perfettamente plastico dopo questa deformazione.
Nella sottostante figura 7 sono riportati gli spostamenti del nodo di estremità (superiore) della mensola e di quello all’attacco della mensola stessa in funzione degli incrementi di carico (si inizia con il solo carico di compressione del pilastro (partendo dal 10% sino al carico totale in assenza del carico sulla mensola). Dall’ undicesimo incremento si introduce il carico sulla mensola con incrementi del 5% e si mantiene inalterato il carico sul pilastro.
La rottura si ha l superamento del sessantaseiesimo incremento. Il coefficiente di sicurezza a rottura vale pertanto 2,8.
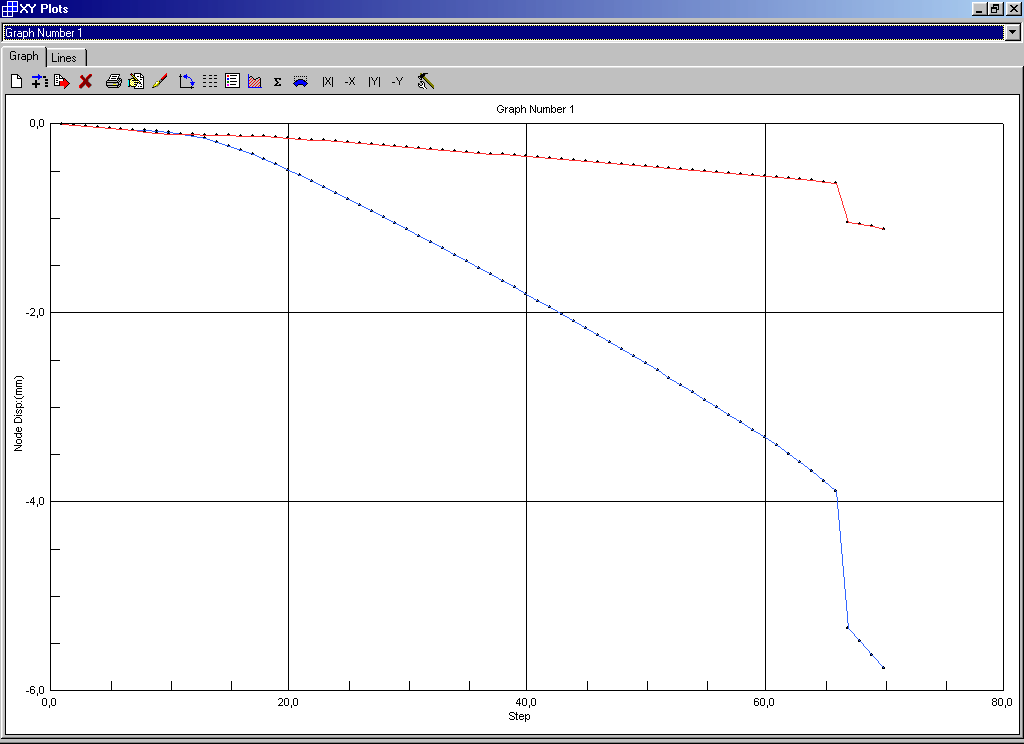
Fig. 7 – Abbassamento dell’estremità della mensola (blu) e del nodo di attacco (rosso).





