Richiami all’ analisi della risposta sismica delle strutture.
Introduzione
Si confrontano brevemente, alla luce di esempi pratici, i diversi metodi che, nella maggior parte delle normative vigenti, sono indicati per lo studio della risposta sismica degli edifici. I metodi in questione sono raggruppati in tre categorie:
La cosiddetta ‘analisi statica equivalente’ è la sola a poter essere affrontata con il calcolo manuale, ed è anche quella più facile da eseguire. Essa è stata quindi quella impiegata più estesamente dagli ingegneri, almeno sino a quando non sono divenute disponibili, ed accessibili risorse di calcolo adeguate (elaboratori e software). L’analisi statica equivalente ha comunque – pur limitata dalla nuova normativa a poche applicazioni – può essere tutt’oggi di utilità per il progettista , almeno in sede di predimensionamento delle strutture. In sede di verifica, l’indicazione predominante – e quella, comunque, relativa alla maggior parte delle strutture in cui ci si imbatte praticamente – suggerisce di utilizzare l’analisi dello spettro di risposta. Addirittura, in alcuni casi, può essere consigliato svolgere l’analisi dinamica nel transitorio, eventualmente anche in modo non-lineare. Nel seguito, discutendo di questi ultimi due metodi si farà riferimento a quanto contenuto nell’ Eurocodice 8 EN 1998 e nella normativa australiana AS1170.4 – 2007. Va da sé che le metodologie trattate sono quelle stesse da utilizzare in applicazione della nuova normativa, ferma restando la formalizzazione dei dati (quali, ad esempio, la scelta dello spettro, o dei fattori di duttilità).
La quantificazione dell’azione sismica
Prima di descrivere i singoli tipi di analisi consentiti, sembra opportuno parlare dei metodi di quantificazione dell’azione sismica utilizzati internazionalmente.
E’ di uso comune qualificare l’intensità di un evento sismico in termini di ‘scala Richter’ o ‘scala Mercalli’. L’ indice Richter per un dato terremoto e’ il logaritmo in base 10 del massimo spostamento verificatosi, misurato in micrometri con un sismografo Wood-Anderson e corretto in una distanza di 100 km. Eventi sismici con indice maggiore di 5 possono provocare danni a strutture.
L’ approccio seguito dalla scala Mercalli (Modified Mercalli), invece, e’ quello di dare una descrizione qualitativa dei danni provocati dal sisma, distinti in una scala di dodici valori, in cui al primo grado corrisponde un sisma non avvertito da alcuno, ed al dodicesimo grado la distruzione totale.
Entrambe questi modi di misurare sinteticamente l’intensità di un terremoto, non sono sufficienti per affrontare il problema dal punto di vista del calcolo strutturale. Per ragionare di concetti e metodi, si può partire dal considerare la risposta dinamica di un sistema ad un grado di libertà (oscillatore semplice).Sistemi ad un grado di liberta’: dall’ accelerogramma allo spettro di risposta
Spesso si conosce, per misura diretta, l’accelerogramma provocato da un sisma. Per passare da questo ad informazioni utilizzabili nel calcolo della risposta di un edificio si fa riferimento alla risposta dell’oscillatore semplice (sistema ad un grado di libertà), immaginando di ‘scomporre’ poi la risposta di una struttura, in quella di tanti ‘oscillatori’ distinti, caratterizzati ciascuno da una propria frequenza (una delle frequenze naturali della struttura stessa).
Fissate le caratteristiche di un oscillatore semplice (vale a dire la sua massa, la sua rigidezza, ed, eventualmente, lo smorzamento), si può determinarne la risposta massima (in termini di accelerazione, velocità e spostamento) rispetto all’ eccitazione dinamica imposta. Si tratta di risolvere l’equazionone differenziale seguente:![]()
dove x e’ il coefficiente di smorzamento viscoso (in genere < 0.1) , w la frequenza naturale e a(t) l’accelerogramma assegnato.
Nel dominio del tempo, l’equazione può essere trattata sia con metodi analitici (integrale di convoluzione) che in forma numerica (differenze finite). Nel secondo caso, ovviamente, la stabilità e la precisione della soluzione dipendono dal metodo scelto, e, nei confronti di questo, dal passo di integrazione adottato. Si può ripetere l’operazione svolta per l’oscillatore semplice campione per altri oscillatori (in sostanza cambiandone la frequenza di vibrazione propria in ragione di massa, rigidezza e smorzamento). Per ciascun oscillatore si disporrà quindi di un valore massimo – nell’intervallo di integrazione utilizzato – per l’accelerazione, la velocità e lo spostamento. Portando in un diagramma detti valori, in funzione della frequenza propria di vibrare dell’ oscillatore semplice (o del periodo proprio), si otterranno i cosiddetti ‘spettri di risposta’ dell’oscillatore semplice, appunto, in termini di accelerazioni, velocità o spostamenti. Il segnale sismico, quand’anche si disponesse di una sua registrazione, è però un segnale random. Quindi non ci si può limitare a considerare lo spettro di risposta così ricavato come base ‘pratica’ per il calcolo. Si può procedere, quindi, in due modi alternativi: - immaginando di disporre di infiniti spettri di risposta, e di utilizzare nel calcolo uno spettro che ne costituisca l’inviluppo; - di calcolare la struttura in transitorio dinamico per un numero rilevante di condizioni di eccitazione descritte tramite specifico accelerogramma (o spostogramma) e di inviluppare le risposte. Dei due metodi il primo si presta ad essere trattato nelle normative in modo abbastanza preciso, e consente, quindi, di delineare una sorta di procedura di verifica definita ‘deterministicamente’. L’inviluppo, infatti, di infiniti spettri di risposta relativi ad un sito tende ad assumere una forma che è caratteristica del sito in cui questi fossero calcolati: dipende, cioè, dal tipo di terreno, dalla stratificazione presente, dalla distanza del fondo roccioso, ecc. Si può, così, pensare di definire (o che una normativa definisca) uno ‘spettro di progetto’, necessariamente convenzionale, ma adeguato all’obiettivo pratico.
Analisi Statica Equivalente
Applicabilita’
L’analisi statica equivalente (negli Euricodici sotto il nome di ‘Analisi modale semplificata con spettro di risposta’) puo’ essere effettuata su edifici che presentano le seguenti caratteristiche normalmente espresse in termini di:
L’ assunzione che sottende l’applicabilità del metodo statico equivalente, è che la struttura risponda dinamicamente come una mensola, e che la quasi totalità della massa sia eccitata in corrispondenza del primo modo di vibrare della stessa (escludendo, quindi, in particolare effetti legati a frequenze fondamentali di tipo torsionale, o ad accoppiamento tra modi flessionali e torsionali caratterizzati da frequenze vicine. Il requisito di regolarità strutturare è fissato proprio per dar corpo a tale assunzione.
Il secondo requisito porta l’ Eurocodice a considerare che gli spostamenti ai piani (e le relative ‘forze sismiche’) crescano linearmente con la distanza dal suolo (a differenza della norma AS1170.4 che fa adottare, per questo tipo di analisi, una distribuzione quadratica di forze e spostamenti ai piani).
Determinazione della forza di taglio sismica totale alla base
La forza di taglio totale alla base dell’edificio viene determinata moltiplicando i carichi permanenti (ai quali viene aggiunta una certa aliquota degli accidentali) per il valore dello spettro di progetto corrispondentemente alla frequenza fondamentale della struttura in questione:
![]()
Tale frequenza deve essere calcolata o stimata con un metodo di riconosciuta validita’. Le normative forniscono formule approssimative per questo calcolo.
Ripartizione della forza sismica su ogni impalcato
La forza di taglio totale sismica alla base viene quindi ripartita su ogni piano tramite il coefficiente di ripartizione dato da:
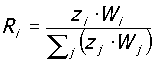
in cui z rappresenta l’altezza del piano considerato e Wi la componente della forza gravitazionale afferente al piano i-esimo. Qualora le masse relative ai vari piani siano uguali, risulta evidente la distribuzione lineare.
La AS1170.4 consente di distribuire la forza di taglio alla base anche per le strutture il cui periodo fondamentale sia maggiore di 2.0 secondi, utilizzando il seguente coefficiente di ripartizione:
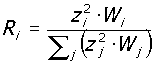
Effetto torsionale
Nella progettazione secondi gli Eurocodici, va tenuto conto di un effetto di torsione, cui partecipano solo i carichi accidentali, trattato mediante un coefficiente che tiene conto dell’eccentricità dei carichi rispetto al baricentro dell’edificio.
La normativa Australiana permette invece di calcolare coerentemente un momento torcente di piano (per edifici di relativa importanza), moltiplicando l’azione calcolata per l’effettiva eccentricita’ tra il centro di taglio e il centro d’ingombro, con correzioni che tengono in contro gli effetti dinamici e le eccentricita’ accidentali.
L’analisi che segue e’ semplicemente elastica lineare, con combinazioni che tengono in conto la possibilita’ che l’evento sismico abbia come direzione una qualunque combinazione delle due direzioni di rigidezza principali (in pianta) dell’edificio. Si noti come la soluzione finale per la combinazione sismica sia equilibrata.
Analisi dello spettro di risposta.
Ipotesi
L’analisi dello spettro di risposta consente uno studio più accurato di quello ottenibile con l’analisi statica equivalente, per una tipologia più generale di strutture. Per la sua applicazione sono necessarie alcune ipotesi:
L’effettivo comportamento non-lineare della struttura (ed, in particolare, il fatto che la struttura abbia un risposta duttile), viene tenuto praticamente in conto (implicitamente nella normativa precedente, in modo esplicito e con maggiori dettagli nella nuova normativa) adottando uno spettro di risposta di progetto ‘duttile’, cioè uno spettro di risposta ridotto rispetto allo spettro elastico che fosse ottenuto come sopra descritto. Tale spettro ‘duttile’ è poi applicato alla struttura assumendo che questa risponde linearmente e che quindi, in particolare, possa esservi applicata la sovrapposizione degli effetti (eventualmente nella forma specifica di sovrapposizione dei modi).
La seconda ipotesi è dovuta al fatto che lo smorzamento e’ trascurato nel calcolo delle frequenze naturali. Per dare un’ordine di grandezza dell’errore presente, si osserva che, per un sistema ad un grado di liberta’, ad esempio, la frequenza fondamentale in presenza di smorzamento e’:
![]()
Se quindi il coefficiente di smorzamento (espresso come rapporto rispetto allo smorzamento critico) e’ minore di 0.1 la differenza tra le due frequenze e’ al piu’ 0.5%.
Implementazione computazionale
Nel seguito si da un breve cenno a come l’analisi dello spettro di risposta è trattata nei codici di calcolo. Una volta calcolati le frequenze proprie (ed i relativi modi) di interessa della struttura, le equazioni del moto risultano ‘disaccoppiate’: è come se ne scrivesse una per ciascuna frequenza propria (cioè per ciascun ‘oscillatore semplice’):
![]()
dove y e’ il vettore delle coordinate modali e K’ e’ la matrice di rigidezza normalizzata. A questo punto si aggiunge lo smorzamento ad ognuna delle equazioni e la forzante e’ scelta come il valore dello spettro di progetto corrispondentemente alla frequenza del singolo oscillatore.
Nel caso in cui lo spettro sia in termini di accelerazioni (lo stesso sarebbe per le velocità o gli spostamenti) la forzante assume la forma:
![]()
con f i autovalore i-esimo, M matrice delle masse, r vettore di direzione del sisma e Si ordinata dello spettro di risposta per la frequenza indagata.
Se infine lo spettro di progetto si riferisce al valore del carico applicato, la forzante diventa:
![]()
con R vettore di carico per una particolare condizione.
Le equazioni disaccoppiate del moto così ricavate vengono risolte in modo semplice, e la soluzione ritrasformata in coordinate fisiche.
![]()
Numero di modi propri di vibrazione
Per ottenere una risposta accurata da un’analisi spettrale, deve essere tenuto in conto un numero di modi propri adeguato. Le norme indicano come ‘adeguato’ il numero di tanti modi quanti sono sufficienti ad eccitare una quota rilevante della massa complessiva (massa strutturale, e masse aggiunte) – ad esempio il 90% -.
I codici di calcolo permettono di verificare questo aspetto, considerando i cosiddetti ‘fattori di partecipazione modale’, che sono gli indicatori, appunto, della quota di massa associata a ciascun modo di vibrare, nelle tre direzioni coordinate.
Si possono presentare, a questo riguardo, alcune complicazioni formali, legate sia alla fisica del problema (e, quindi, alla geometria della struttura considerata e relativa distribuzione delle masse), che al modo con cui la struttura stessa viene discretizzata nel modello ad elementi finiti. Un esempio che può chiarire questo problema è quello del sisma con accelerazione verticale.
Le frequenze proprie di vibrazione della struttura in senso verticale possono essere raggruppate in due ‘famiglie’:
Complessivamente:
In senso pratico:
E’ poi evidente che, nella combinazione tra azioni verticali ed azioni orizzontali, la risposta di ‘travi’ e ‘pilastri’ è ben diversa: per questi ultimi un incremento di carico verticale può essere di aiuto, anziché di danno.
Per approfondire la discussione su questo tema, ci si riferisca all’esempio seguente.
Esempio
Si consideri la struttura a portale evidenziata in figura soggetta ad un sisma con direzione verticale. Essa e’ un semplice telaio piano di altezza 6 m, larghezza 5 m.
Per tale struttura le frequenze naturali che, in caso di sisma verticale, ‘eccitano’ la maggior parte delle masse sono le seguenti:
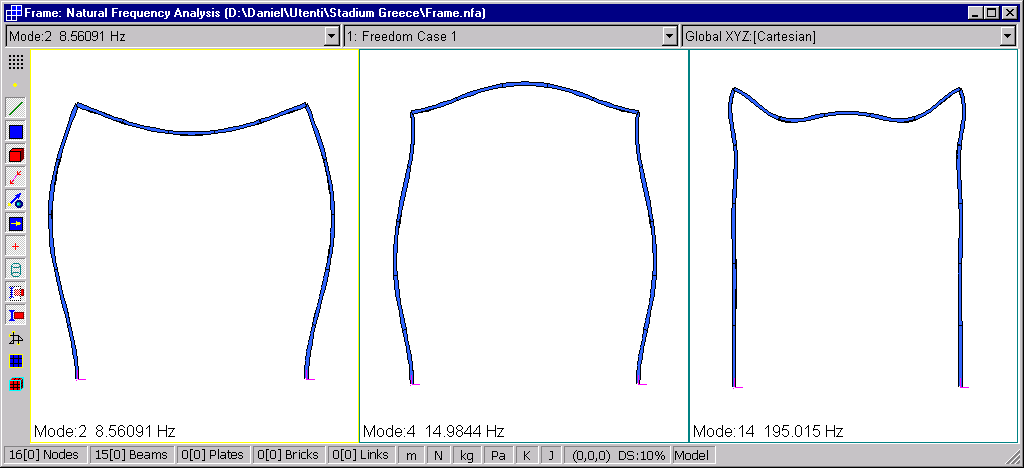
come si può affermare dopo aver lanciato in Straus7 lo ‘Spectral Solver’ ed aver calcolato la massa eccitata in corrispondenza di ciascun modo, come si può vedere dall’estratto del Log file.
EXCITATION FACTORS
Mode Excitation Amplitude Participation (%)
1 1.638919E-15 2.448030E-17 0.000
2 1.731137E+01 1.495795E-02 8.540
3 7.394676E-14 2.817129E-17 0.000
4 2.212920E+01 4.995576E-03 13.955
5 2.944856E-11 1.244316E-15 0.000
6 4.858872E+00 1.762342E-04 0.673
7 3.813599E-11 7.171120E-16 0.000
8 5.671975E-01 5.109340E-06 0.009
9 1.183167E-10 9.264109E-16 0.000
10 9.762941E+00 4.490351E-05 2.716
11 2.925012E-10 1.107574E-15 0.000
12 6.661620E+00 2.416929E-05 1.265
13 1.021053E-11 1.917199E-17 0.000
14 4.736429E+01 3.397340E-05 63.928
15 3.738907E-12 2.675485E-18 0.000
16 8.956269E-02 1.439609E-08 0.000
17 1.506789E+01 1.232426E-06 6.470
18 8.143820E-08 6.660660E-15 0.000
19 1.597571E-06 6.696231E-14 0.000
20 7.913091E+00 2.601720E-07 1.784
TOTAL MASS PARTICIPATION: 99.339%
Si vede come il modo 14 coinvolge circa il 64% delle masse, ed è associato all’oscillazione assiale dei pilastri.
Sono state analizzate due soluzioni spettrali: nella prima si sono inclusi solo i modi 2 e 4, con un valore del ‘total mass participation’ di solo il 22.5%; nella seconda sono stati inclusi i modi 2, 4 e 14 , raggiungendo l’86.42% di massa partecipata.
Come si puo’ vedere dai risultati in termini di spostamenti le due soluzioni sono praticamente coincidenti. Questo perche’ l’ampiezza di oscillazione assiale delle colonne e’ estremamente piccola se comparata a quella flessionale della trave. Lo si dimostra nella figura seguente.
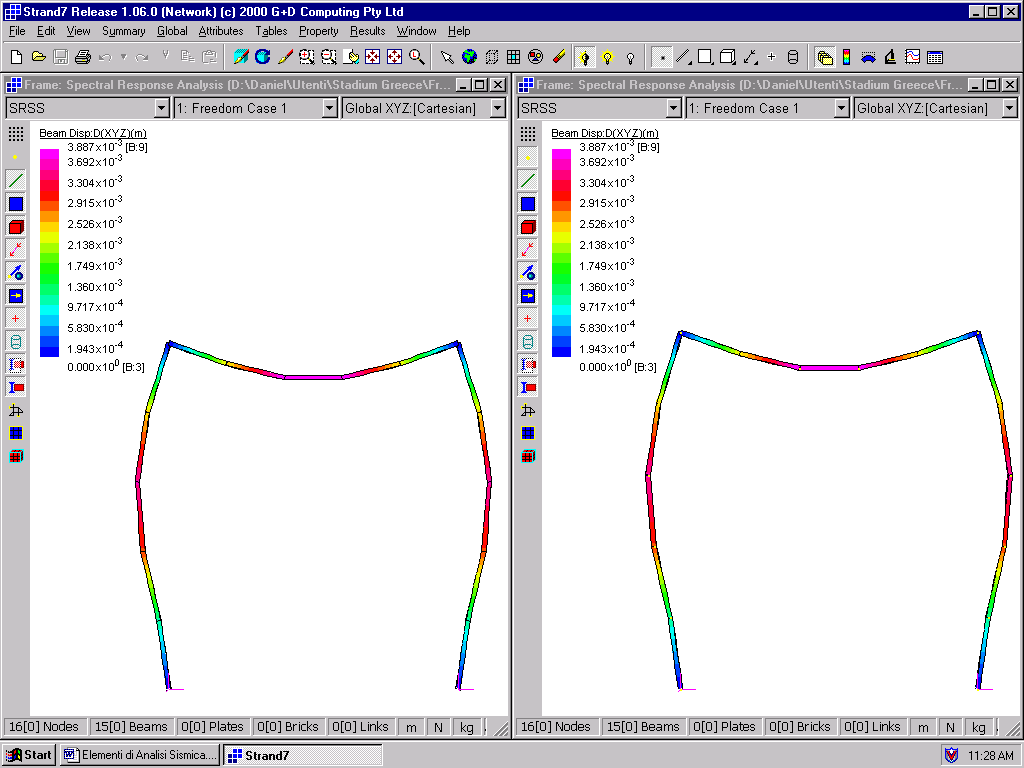
Sovrapposizione delle singole risposte modali
Una volta analizzata la risposta della struttura nei singoli modi di vibrare, occorre combinare i risultati per ottenere la massima sollecitazione possibile (o il massimo spostamento se interessano gli stati limiti di utilizzo). Questo problema non e’ di facile soluzione in quanto nell’istante in cui un modo raggiunge massima ampiezza, un altro puo’ avere ampiezza molto inferiore rispetto al proprio massimo: in generale è estremamente improbabile che tutti i modi siano in fase, e se lo sono, lo sono comunque per un solo istante. La semplice sovrapposizione dei risultati (cioè la loro somma diretta) si traduce quindi in una sovrastima dei valori, che può risultare anche considerevole, se la massa partecipata è ‘distribuita’ su un certo numero di modi.
Una combinazione frequentemente adottata è quella cosiddetta SRSS (o radice quadrata della somma dei quadrati) in cui per risposta massima viene intesa la norma euclidea delle risposte corrispondentemente ai singloli modi :
![]()
Tale modalita’ di combinazione e’ ritenuta valida dalle norme solo se le singole frequenze allo studio sono sufficientemente distanziate, dando più precisamente limiti del tipo: se fi e fj sono due frequenze successive con fi < fj deve essere fi < 0.9fj . Infatti, se due (o più) frequenze sono tra loro abbastanza vicine, la probabilità (in senso ‘ingegneristico’) che esse sia in fase è maggiore (è maggiore l’intervallo temporale in cui esse possono essere prossime ad essere in fase).
Per tener conto di questo aspetto, è proposta la combinazione di tipo CQC (o combinazione quadratica completa:
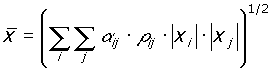
La combinazione di tipo CQC e’ una generalizzazione di quella SRSS - e tiene conto del grado di correlazione esistente tra i diversi modi propri - con cui coincide nel caso in cui le frequenze siano sufficientemente distanziate tra loro.
E’ importante notare come la combinazione finale sia in generale non equilibrata: i ‘massimi’ ottenuti con le combinazioni appena descritte, sono relativi a combinazioni di valori che riferiscono, per gli elementi concorrenti in un punto, ad istanti diversi.
Analisi dinamica nel transitorio.
Applicabilita’
Si tratta del metodo che, sotto il profilo teorico, è più corretto, poiché tratta la risposta della struttura nel dominio del tempo, relativamente all’azione di un accelerogramma di progetto. Non sono più necessarie le ipotesi fatte in precedenza circa la linearità e gli effetti dello smorzamento. Le varie non-linearità, quali le non-linearità legate al materiale (ad esempio formazione di cerniere plastiche negli elementi inflessi) od alla geometria (e.g. comportamento di sistemi composti di funi) possono essere tenute in conto senza necessità di ulteriori approssimazioni.
Unica controindicazione dal punto di vista numerico e’ il tempo di soluzione. Utilizzando infatti un solutore di tipo implicito (incondizionatamente stabile) occorre risolvere un sistema lineare per ogni passo temporale. In presenza di non linearita’ il tempo aumenta considerevolmente a causa delle iterazioni che portano alla configurazione equilibrata.
Utilizzando peraltro un solutore di tipo esplicito, il tempo per la determinazione del singolo passo temporale e’ estremamente breve, ma la stabilita’ del metodo e’ assicurata solamente per incrementi di tempo piuttosto contenuti.
Esempio comparativo
Nel seguente esempio si vogliono applicare i tre tipi di analisi descritti ad un edificio, per una comparazione critica sia dei risultati sia della mole di calcolo preparatorio richiesta da ciascuno.
La geometria dell’edificio e’ descritta nel seguito:
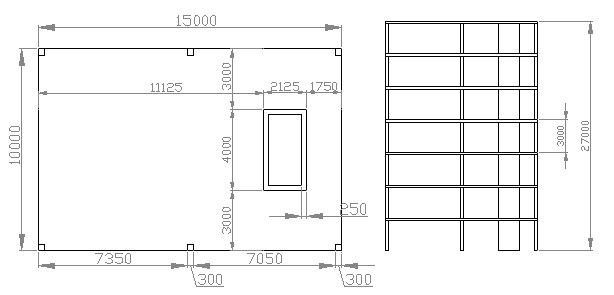
Determinazione dello spettro di risposta
Prima di iniziare le calcolazioni per l’analisi statica occorre determinare lo spettro di progetto a cui riferirsi. Esso viene ricavato direttamente dall’accelerogramma corrispondente al famoso terremoto di El Centro, in figura, e per semplicita’ non viene applicato alcun coefficiente correttivo.
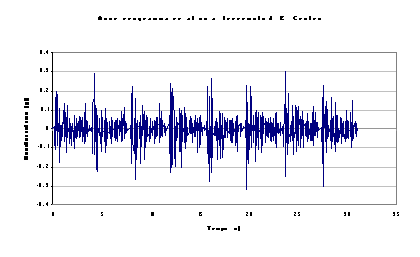
Utilizzando uno schema alle differenze finite per la risoluzione dell’equazione corrispondente ad un singolo grado di liberta’ (si e’ scelto lo schema generale di collocation con cefficienti g = 0.5 e b = 0.25) e considerando un rapporto di smorzamento del 5% si ottiene lo spettro voluto.
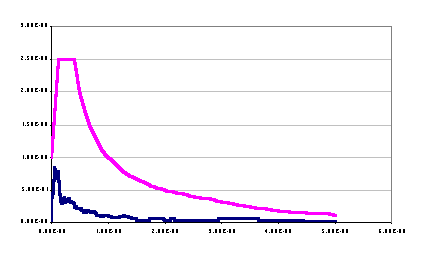
Nel grafico in figura sono posti a confronto lo spettro ottenuto da calcolazioni dirette con quello offerto dall’Eurocodice 8 per un terreno aventi caratteristiche classificabili come A.
Analisi Statica Equivalente
All’edificio scelto vengono ora applicate opportune forze statiche per simulare l’effetto flessionale e torsionale del sisma. Sebbene le carattistiche di regolarita’ espresse nell’Eurocodice 8 non siano soddisfatte (in particolare il vano scala controventante in calcestruzzo armato e’ disposto in posizione non simmetrica), sono introdotti momenti torcenti di piano in accordo alla normativa australiana.
Il primo passo necessario e’ la determinazione della frequenza fondamentale dell’edificio. L’analisi delle frequenze naturali dell’edificio, restituisce i seguenti valori:
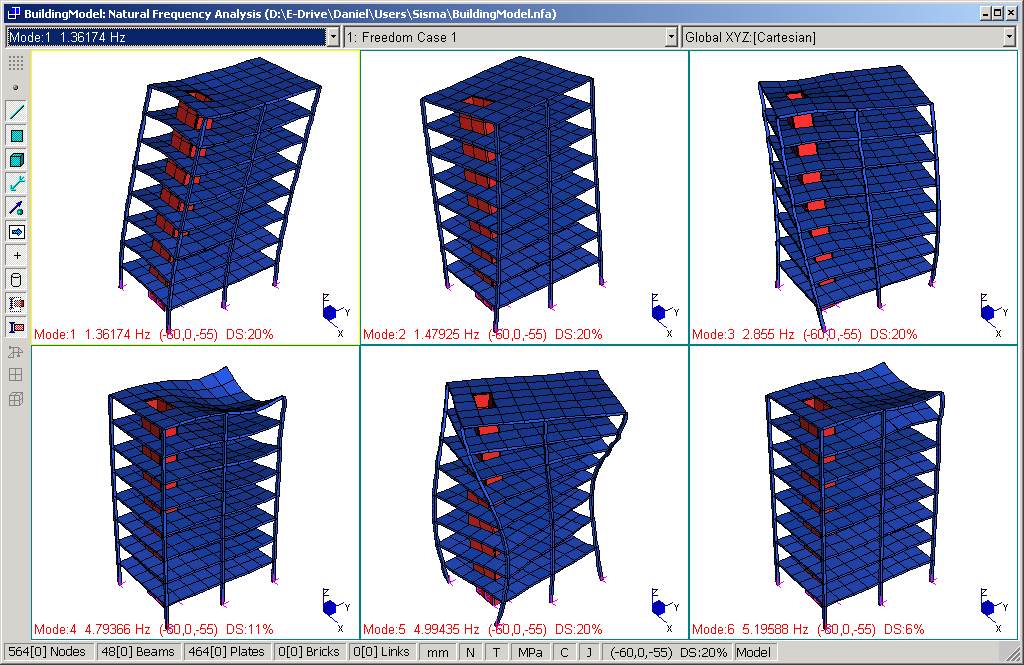
Su tali frequenze e’ stato inoltre effettuato uno studio di convergenza, infittendo progressivamente la mesh.
La somma dei carichi gravitazionali totali e’ di circa 705 T. Considerando il valore dello spettro di risposta, calcolato e prescritto, corrispondente ai periodi calcolati si ottiene il seguente valore dello sforzo di taglio massimo alla base:
|
Sforzo di Taglio alla Base [kN] |
||
|
|
|
|
|
|
Spettro Calcolato |
Eurocodice 8 |
|
Primo Periodo |
302 |
4533 |
|
Secondo Periodo |
747 |
5562 |
Tale forza va dunque distribuita linearmente con l’altezza secondo la formula:
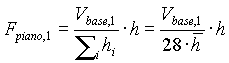
Ripetendo le calcolazioni per la frequenza naturale relativa al sisma nella direzione ortogonale (che genera torsione) si ha:
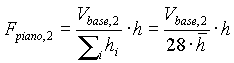
Per la rappresentazione degli effetti torsionali e’ importante calcolare l’eccentricita’ tra il baricentro geometrico (baricentro della pianta) ed il centro di taglio dell’edificio.
Il centro di taglio e’ esprimibile utilizzando la seguente formulazione:
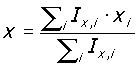
Ove Ix,i e’ il momento d’inerzia del singolo elemento strutturale (distante xi dal riferimento) rispetto al proprio baricentro.
L’eccentricità ricavata risulta: e = 4.66 m
Si possono ora applicare le forze statiche equivalenti e verificare le sollecitazioni sui vari elementi strutturali.
Analisi dello spettro di risposta
Una volta individuato lo spettro di progetto, occorre semplicemente impostare gli opportuni parametri del solutore.
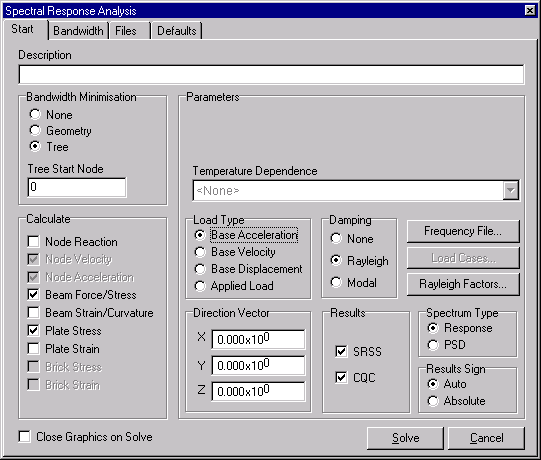
Tipo di Forzante (Load Type)
Permette di specificare a quale tipo di forzante esterna corrisponde lo spettro di risposta scelto.
Smorzamento (Damping)
Si può scegliere tra due tipi di smorzamento: smorzamento di Rayleigh e smorzamento modale. Nel caso di smorzamento modale si può precisare direttamente per ogni frequenza naturale lo smorzamento da applicare.
Scegliendo ‘Rayleigh’ lo smorzamento del sistema viene definito come una combinazione della sua massa e della sua rigidezza. Tale approccio attribuisce lo smorzamento a ciascuna frequenza propria secondo una legge quadratica, definita utilizzando due punti (coppie frequenza, rapporto di smorzamento).
Direzione (Direction Vector)
Esso rappresenta il vettore di direzione del sisma. Se lo spettro e’ normalizzato deve essere incluso il valore di picco.
File di analisi delle frequenze proprie (Frequency File)
Tale finestra di dialogo consente di specificare, in forma tabulare, quali modi devono essere inclusi, la curva spettrale relativa, ed il rapporto di smorzamento opportuno.
Analisi dinamica nel transitorio.
Per operare un’analisi dinamica nel transitorio e’ necessario specificare la storia di accelerazione alla base dell’edificio e specificare i parametri rilevati nella finestra di dialogo del solutore.
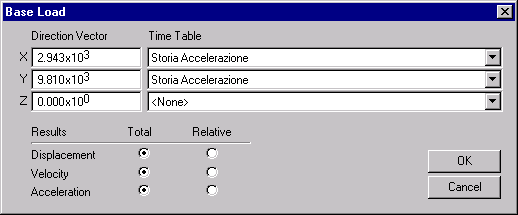
Forzante agente alla base (Base Load)
Tale finestra di dialogo consente di specificare la storia dell’accelerazione esterna oltre che la direzione di riferimento. Si puo’ inoltre scegliere se si vogliono i risultati (grandezze cinematiche) espressi in valore assoluto o relativamente a quelli alla base della struttura. Ovviamente parametri di sollecitazione e tensioni non cambiano con questa scelta.
Comparazione critica dei risultati ottenuti
I risultati ottenuti dalle singole analisi sono confrontati sul valore del massimo momento flettente nelle due direzioni principali, in senso assoluto, e relativamente a quelli del pilastro più sollecitato nell’analisi dinamica nel transitorio.
Sia per l’analisi spettrale che per l’analisi statica equivalente sono stati considerati due valori per lo spettro di progetto.
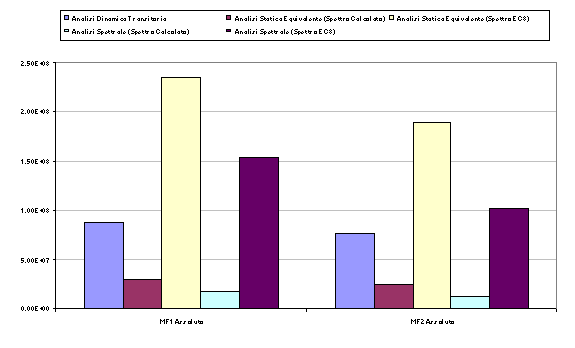
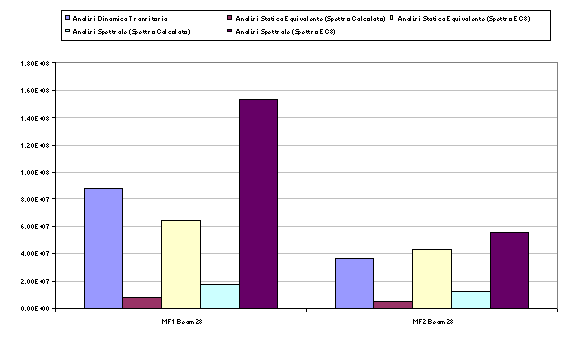
Risulta evidente come utilizzando lo spettro calcolato direttamente dalla storia delle accelerazioni si sottostimino i valori delle sollecitazioni flettenti. Se infatti i massimi di accelerazione relativi a due oscillatori differenti capitano allo stesso momento e sono in fase, essi vengono sommati nell’analisi dinamica transitoria, e combinati SRSS dalla spettrale (il risultato e’ quindi minore).
Dal caso presentato, si evince che, da un punto di vista di accuratezza, una seconda scelta dopo l’analisi della risposta nel transitorio e' senz’altro quella dello spettro di risposta, che produce, con tempi di calcolo molto inferiori, risultati conservativi. Essa consente inoltre di evitare il calcolo manuale del sistema di forze statiche equivalenti, come anche quello di grandezze geometriche, quali il centro di taglio.
Per inviare un messaggio: hsh@iperv.it