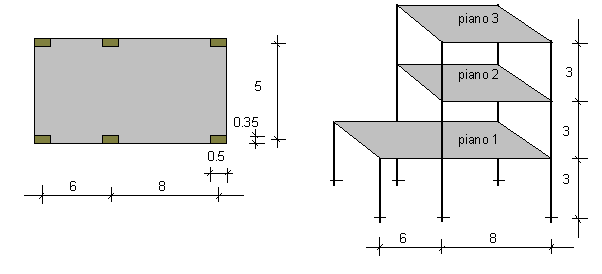

BEAM PROPERTIES TOTAL = 1 TYPE = 1 Section
Standard: Solid Rectangle (D= 5.000E-01 B= 3.500E-01)
Beam Type: Normal Beam
E = 3.0000E+07 A = 1.7500E-01
J = 4.1765E-03 G = 0.0000E+00
I11 = 3.6458E-03 I22 = 1.7864E-03
Shear:L1 = 0.0000E+00 Shear:L2 = 0.0000E+00
NodLine:L1 = 0.0000E+00 NodLine:L2 = 0.0000E+00
UDL:1 = 0.0000E+00 UDL:2 = 0.0000E+00
TG:1 = 0.0000E+00 TG:2 = 0.0000E+00
Alpha = 0.0000E+00 SA11 = 0.0000E+00
Density = 0.0000E+00 SA22 = 0.0000E+00
Temperature Table = 0
PLATE PROPERTIES TOTAL = 1 TYPE = 1
ISOTROPIC Element : LinearQuad, PlateShell, Von Mises
E = 3.0000E+07
Poisson Ratio = 1.5000E-01
Alpha = 0.0000E+00
Layers No. = 0
Memb.Thick = 2.0000E-01 Bend.Thick = 2.0000E-01
Pressure = 0.0000E+00 Density = 4.2500E+00
Stress:1 = 0.0000E+00 Stress:2 = 0.0000E+00
Stress:3 = 0.0000E+00 Stress:4 = 0.0000E+00
Shear :1 = 0.0000E+00 Shear :2 = 0.0000E+00
Shear :3 = 0.0000E+00 Shear :4 = 0.0000E+00
Temperature Table = 0
Stress-Strain Table = 0
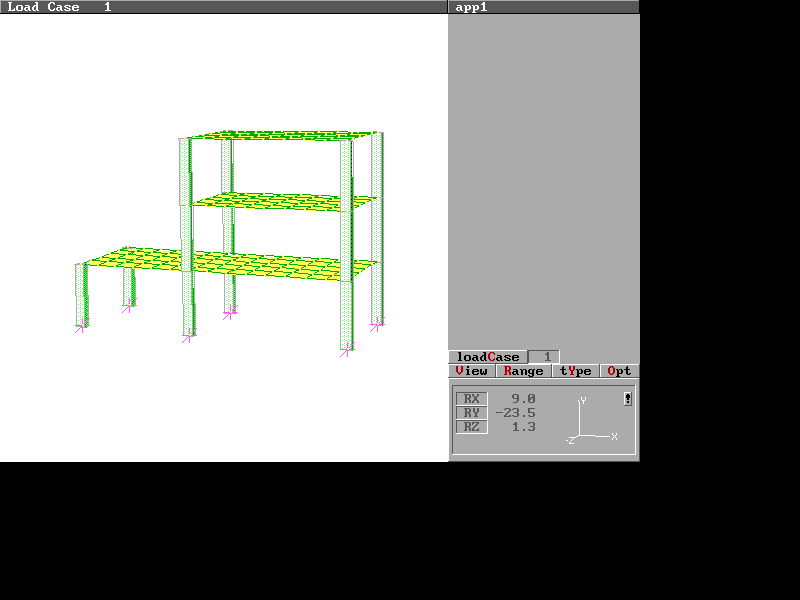
Analisi modale
Vengono calcolati i primi 10 modi. La matrice delle masse è diagonale (lumped).
No. EIGENVALUES NATURAL FREQ. NATURAL FREQ.
(RAD/SEC) (CYCLES/SEC)
1) 1.0982444749E+02 1.0479716002E+01 1.6678986040E+00
2) 1.3993627414E+02 1.1829466351E+01 1.8827180439E+00
3) 4.1727154224E+02 2.0427225515E+01 3.2510939144E+00
4) 1.1719032547E+03 3.4233072528E+01 5.4483627102E+00
5) 1.2484357046E+03 3.5333209656E+01 5.6234549722E+00
6) 1.3189963162E+03 3.6317988879E+01 5.7801874534E+00
7) 1.4303474729E+03 3.7819934861E+01 6.0192295807E+00
8) 2.0437385632E+03 4.5207726808E+01 7.1950331877E+00
9) 2.7462141186E+03 5.2404333014E+01 8.3404086388E+00
10) 3.4616033328E+03 5.8835391839E+01 9.3639434401E+00
No. NATURAL FREQ. PERIOD
(CYCLES/SEC) (seconds)
1) 1.6678986040E+00 0.599557
2) 1.8827180439E+00 0.531147
3) 3.2510939144E+00 0.307589
4) 5.4483627102E+00 0.183541
5) 5.6234549722E+00 0.177827
6) 5.7801874534E+00 0.173005
7) 6.0192295807E+00 0.166134
8) 7.1950331877E+00 0.138985
9) 8.3404086388E+00 0.119898
10) 9.3639434401E+00 0.106793
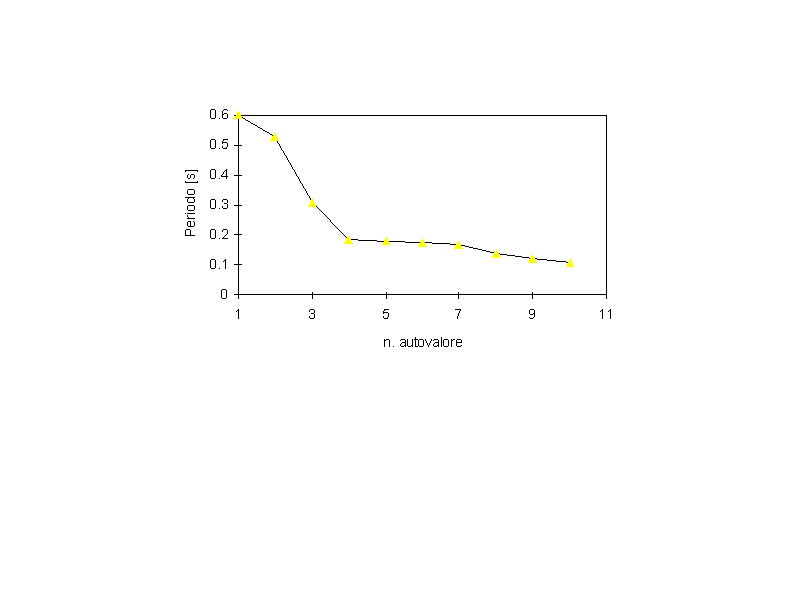
Periodi fondamentali associati ai primi 10 autovalori (frequenze).
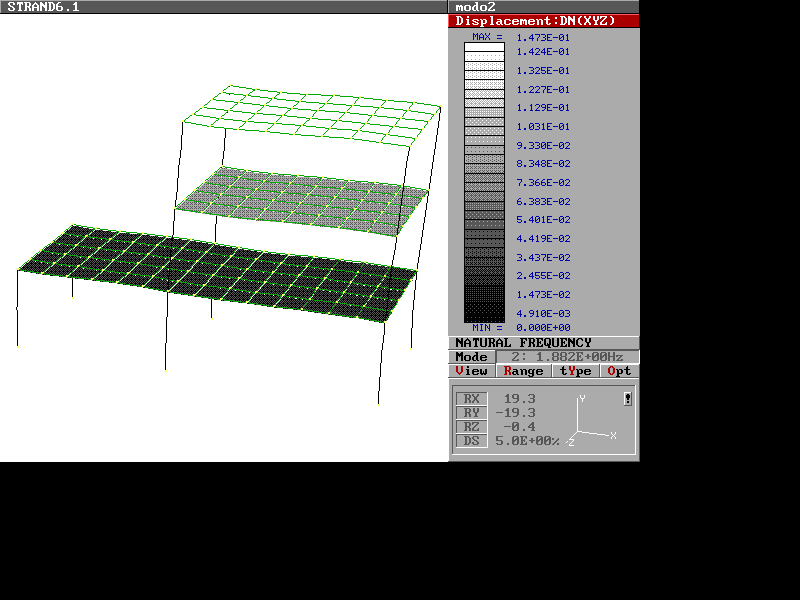
Modo n. 2
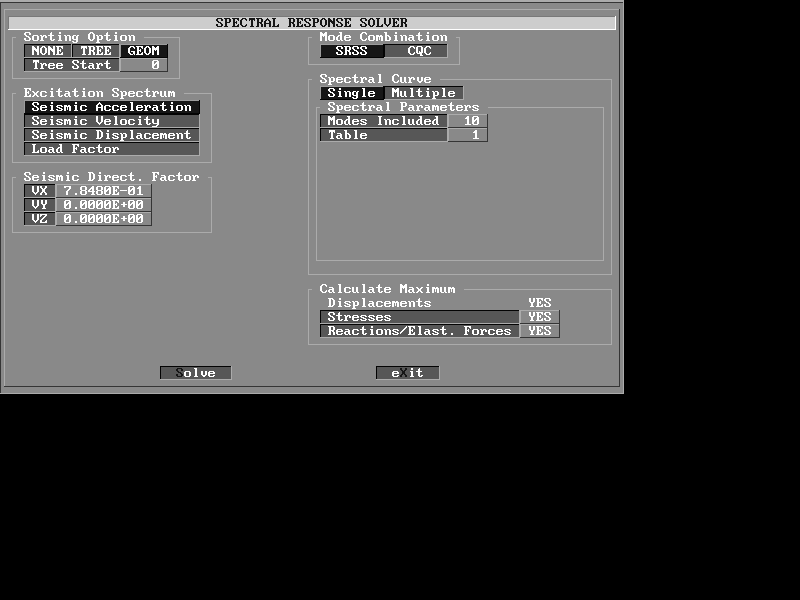
Modo n. 8
Introduzione dello spettro
La normativa italiana fornisce la seguente relazione (§C.6.1.1.):
- per T0 > 0.8 s R = 0.862 / T02/3
- per T0 £ 0.8 s R = 1.0
con:
R(T) coefficiente di risposta
T periodo fondamentale
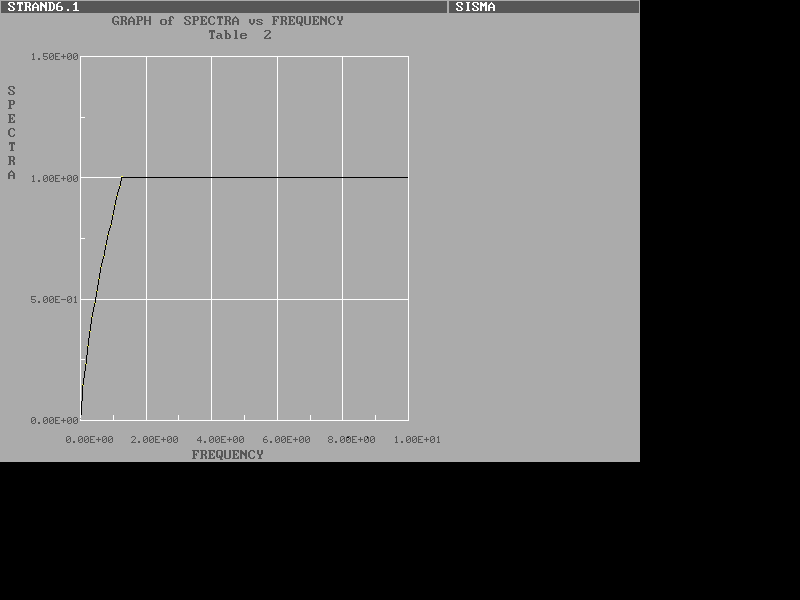
Il coefficiente di risposta è rappresentato nel grafico che segue:
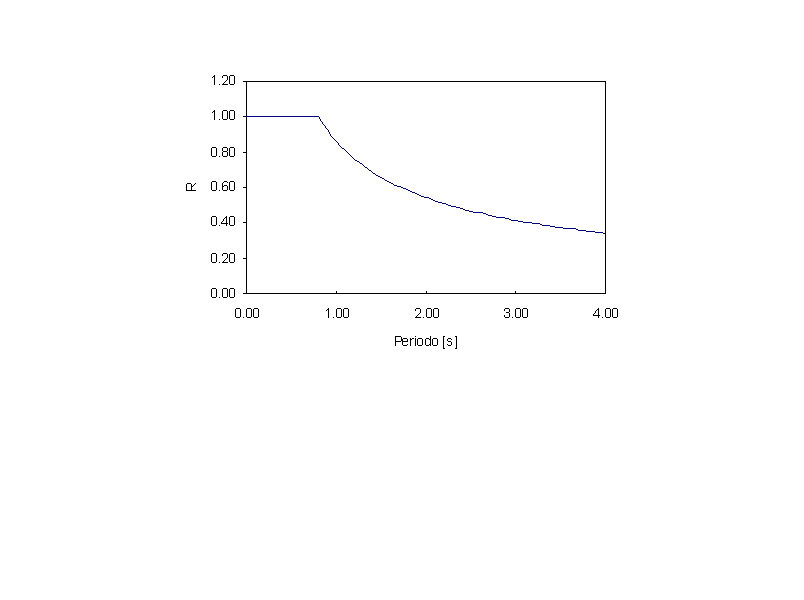
E' necessario una trasformazione della variabile indipendente da periodo a frequenza:
- per f0 < 1.25 Hz R = 0.862 / ( 1/f0 )2/3
- per f0 ³ 1.25 Hz R = 1.0
con f0 = 1/T0
La relazione, introdotta nel modulo "Tables Input" - "Time Factor - Spectral" - "Spectral Table", permette di definire la curva spettrale a meno del moltiplicatore
m = C e b I g =0.08 x 1.0 x 1.0 x 1.0 x 9.81 = 0.7848
La relazione introdotta è: 0.862 / (1/f)^(2/3). Il tratto costante è stato inserito
manualmente.
FREQUENCY= 0.0000E+0000, SPECTRA= 0.0000E+0000
FREQUENCY= 6.9444E-0002, SPECTRA= 1.4563E-0001
FREQUENCY= 1.3889E-0001, SPECTRA= 2.3118E-0001
FREQUENCY= 2.0833E-0001, SPECTRA= 3.0293E-0001
FREQUENCY= 2.7778E-0001, SPECTRA= 3.6698E-0001
FREQUENCY= 3.4722E-0001, SPECTRA= 4.2584E-0001
FREQUENCY= 4.1667E-0001, SPECTRA= 4.8088E-0001
FREQUENCY= 4.8611E-0001, SPECTRA= 5.3292E-0001
FREQUENCY= 5.5556E-0001, SPECTRA= 5.8254E-0001
FREQUENCY= 6.2500E-0001, SPECTRA= 6.3013E-0001
FREQUENCY= 6.9444E-0001, SPECTRA= 6.7598E-0001
FREQUENCY= 7.6389E-0001, SPECTRA= 7.2032E-0001
FREQUENCY= 8.3333E-0001, SPECTRA= 7.6334E-0001
FREQUENCY= 9.0278E-0001, SPECTRA= 8.0518E-0001
FREQUENCY= 9.7222E-0001, SPECTRA= 8.4596E-0001
FREQUENCY= 1.0417E+0000, SPECTRA= 8.8578E-0001
FREQUENCY= 1.1111E+0000, SPECTRA= 9.2472E-0001
FREQUENCY= 1.1806E+0000, SPECTRA= 9.6286E-0001
FREQUENCY= 1.2500E+0000, SPECTRA= 1.0003E+0000
FREQUENCY= 1.0000E+0001, SPECTRA= 1.0000E+0000
Il coefficiente di risposta deve essere moltiplicato per il coefficiente m per ottenere
lo spettro delle accelerazioni.
Questo viene fatto, per comodità, direttamente definendo la direzione del sisma come:
VX = 0.7848
VY = 0
VZ = 0
Alternativamente si sarebbe potuto definire direttamente lo spettro delle accelerazioni
in "Spectral Table" inserendo la relazione 0.7848 x 0.862 / (1/f)^(2/3); in tal caso si
doveva porre:
VX=1, VY=0, VZ=0
Viene utilizzato il metodo SRSS. La schermata del solutore è la seguente:
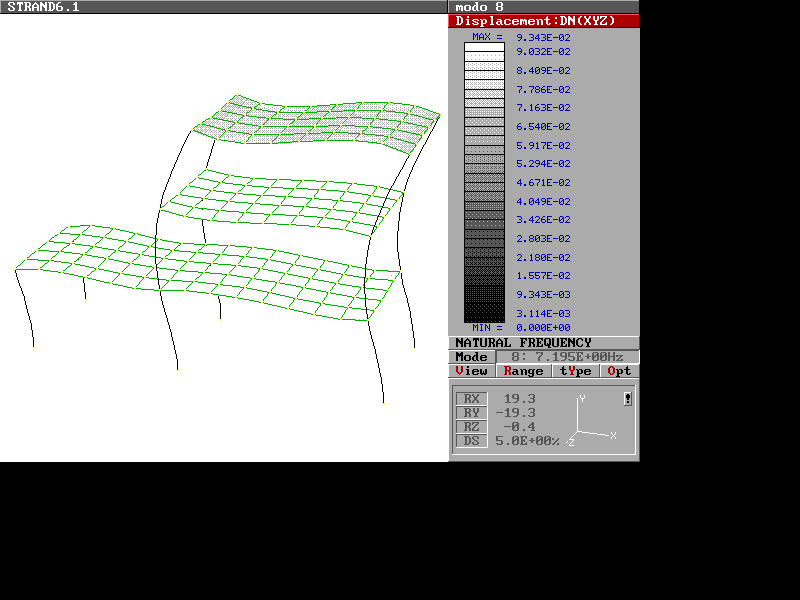
Il file log "FileName.PLG" è il seguente:
STRAND6.15 SPECTRAL RESPONSE SOLVER
Solution Started 08:56:54 on 29/11/95
File : C:\STRAND61\SISMA
Heading : STRAND6.1
207 Nodes. 14 Beams. 150 Plates. 0 Bricks.
WARNING! Thermal loads are ignored since the
Node Temperature File does not exist.
Load Cases = 2
Consistent Load Vector for Beam UDLs.
Lumped Load Vector for Plate Pressure.
Lumped element mass matrices.
Plate Drilling Freedoms are Suppressed.
Sorting Nodes : GEOM METHOD
Sort order : ZYX
PASS NUMBER 1
Maximum Beam Bandwidth = 60
at Beam Number = 6
Maximum Plate Bandwidth = 138
at Plate Number = 25
PASS NUMBER 2
Maximum Beam Bandwidth = 38
at Beam Number = 5
Maximum Plate Bandwidth = 106
at Plate Number = 25
Total Disk Space Required = 3.120 MB
Total Disk Space Available = 248.447 MB
... Creating Matrix. 20 Blocks.
... Sorting Elements.
... Calculating Spectral Values
Assembling 14 Beams.
WARNING! Beam Property Type 1 has Zero Shear Modulus.
... Beam Assembly Complete.
Assembling 150 Plates.
... Plate Assembly Complete.
... Executing Spectral Response Solver.
MASS MATRIX: LUMPED
EXCITATION SPECTRUM: SEISMIC ACCELERATION
SEISMIC DIRECTION FACTORS
X Y Z
0.784800 0.000000 0.000000
MODE FREQUENCY (Hz) TABLE NO. SPECTRAL VALUE
1 1.667899 1 1.757893
2 1.882718 1 1.905581
3 3.251094 1 2.499984
4 5.448363 1 2.499986
5 5.623455 1 2.499987
6 5.780187 1 2.499987
7 6.019230 1 2.499987
8 7.195033 1 2.499988
9 8.340409 1 2.499989
10 9.363943 1 2.499990
... Calculating Mass Participation Factors.
Total Disk Space Required = 0.096 MB
Total Disk Space Available = 247.300 MB
... Reducing 10 Eigenvectors for non-active degrees of freedom.
SEISMIC EXCITATION FACTORS & MASS PARTICIPATION FACTORS
MODE EXCITATION MASS.PARTIC. (%)
1 0.000000 ( 0.535327E-011) 0.00
2 7.211118 ( 0.721112E+001) 66.22
3 0.000000 ( 0.804493E-011) 0.00
4 0.002862 ( 0.286188E-002) 0.00
5 0.007211 ( 0.721131E-002) 0.00
6 0.000000 ( 0.181547E-008) 0.00
7 0.173255 ( 0.173255E+000) 0.04
8 4.673290 ( 0.467329E+001) 27.81
9 0.000008 ( 0.756272E-005) 0.00
10 0.085366 ( 0.853657E-001) 0.01
Total Mass Participation Factor: 94.08 %
MODAL DISPLACEMENT AMPLITUDE
MODE AMPLITUDE
1 0.000000 ( 0.856866E-013)
2 0.098197 ( 0.981974E-001)
3 0.000000 ( 0.481993E-013)
4 0.000006 ( 0.610517E-005)
5 0.000014 ( 0.144406E-004)
6 0.000000 ( 0.344099E-011)
7 0.000303 ( 0.302817E-003)
8 0.005717 ( 0.571657E-002)
9 0.000000 ( 0.688465E-008)
10 0.000062 ( 0.616516E-004)
... Maximum Displacements, Modal Combination SRSS.
Combining 2 Blocks
... Beam Stresses for Mode 1
... Beam Stresses for Mode 2
... Beam Stresses for Mode 3
... Beam Stresses for Mode 4
... Beam Stresses for Mode 5
... Beam Stresses for Mode 6
... Beam Stresses for Mode 7
... Beam Stresses for Mode 8
... Beam Stresses for Mode 9
... Beam Stresses for Mode 10
... Plate Stresses for Mode 1
... Plate Stresses for Mode 2
... Plate Stresses for Mode 3
... Plate Stresses for Mode 4
... Plate Stresses for Mode 5
... Plate Stresses for Mode 6
... Plate Stresses for Mode 7
... Plate Stresses for Mode 8
... Plate Stresses for Mode 9
... Plate Stresses for Mode 10
STRAND6.15 SPECTRAL REACTION RECOVERY
File : C:\STRAND61\SISMA
Heading : STRAND6.1
207 Nodes. 14 Beams. 150 Plates. 0 Bricks.
Applied Loads are Not Included.
... Sorting Elements.
Assembling 14 Beams.
WARNING! Beam Property Type 1 has Zero Shear Modulus.
... Beam Assembly Complete.
Assembling 150 Plates.
... Plate Assembly Complete.
E' importante controllare i messaggi di esecuzione. In particolare si noti che più del
90% della massa complessiva è stata introdotta nell'analisi: il numero di modi considerati
risulta cioè sufficiente.
Si noti anche che si sarebbero potuti introdurre solo i modi 2,8,7, ottenendo lo stesso
risultato.
La figura che segue visualizza una schermata di risultati.
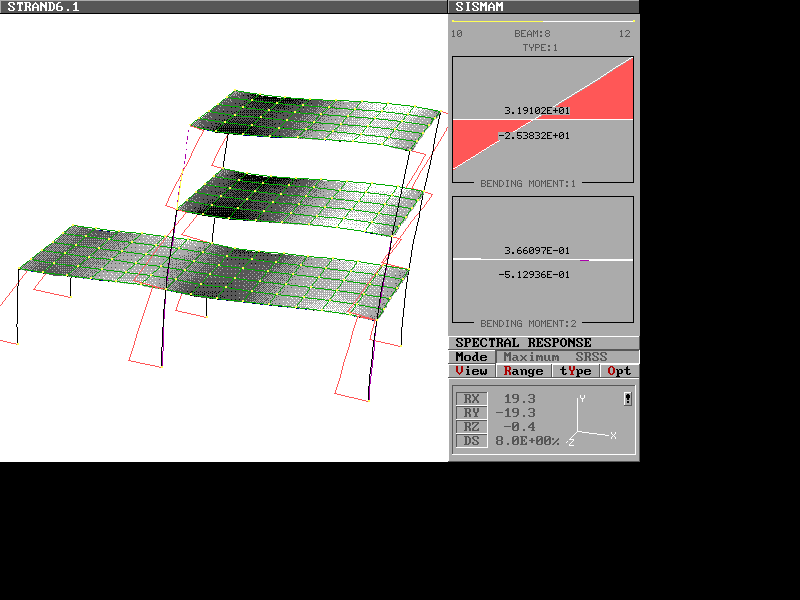
Diagramma dei momenti flettenti (M11) e deformata.