Università degli Studi di Padova – Facoltà di Ingegneria
DIPARTIMENTO DI COSTRUZIONI E TRASPORTI
Sviluppo e validazione di un modello non lineare
per la
determinazione del fattore di struttura “q”
di edifici in
legno a parete massiccia tipo X-Lam
ING. POZZA LUCA - ING. SCOTTA ROBERTO - ING. SECCHI STEFANO
INTRODUZIONE -
Il sistema costruttivo XLam sta avendo una larga diffusione grazie alle sue ottime caratteristiche e
prestazioni. La sostenibilità e la convenienza dei moderni edifici in legno è legata sempre più al
fatto che essi sono integrati con dispositivi e soluzioni costruttive finalizzate al basso consumo
energetico in fase di gestione dell’edificio; ciò rende questa tipologia competitiva, efficiente e
sicura rispetto ad altre tipologie più classiche.
Dal punto di vista sismico gli edifici XLam manifestano un buon comportamento grazie alla loro
leggerezza e ad una buona capacità di dissipazione energetica. Le forze indotte dal sisma nella
struttura risultano infatti proporzionali alla massa ed inversamente proporzionali alla capacità di
dissipare energia. Il legno presenta un rapporto resistenza/peso molto vantaggioso se paragonato a
quello del calcestruzzo con il vantaggio che resiste anche a sforzi di trazione.
Nella pratica costruttiva i vari elementi lignei che costituiscono la struttura portante degli edifici
XLam vengono assemblati mediante connessioni di tipo metallico. Tali elementi di connessione, se
progettati in modo corretto, manifestano un comportamento duttile che va a conferire al sistema
“legno + connessione” un’ottima resistenza e robustezza alle azioni cicliche e quindi al sisma.
Nonostante questo sistema costruttivo sia diffuso nella pratica comune, nessuna indicazione
costruttiva o di calcolo è contenuta all’interno delle normative nazionali ed internazionali.
Indagini e ricerche, allo scopo di ottenere dati certi che possano costituire un valido supporto per
l’inserimento del sistema nelle prescrizioni normative, sono in corso soprattutto per quanto riguarda
lo studio della risposta all’azione sismica. Il più importante progetto di ricerca in Italia in atto è il
PROGETTO SOFIE finanziato dalla provincia autonoma di Trento e coordinato dal CNR-IVALSA.
Tale progetto si compone di prove sperimentali (monotone e cicliche) sui singoli elementi di
connessione e pannelli pareti. I risultati di tali prove sperimentali sono riportati in [1]. Significativi
sono i test dinamici condotti su edifici multipiano in XLam in scala reale su tavola vibrante. Tali
test sono stati accompagnati da simulazioni numeriche in ambito non lineare allo scopo di simulare
la loro risposta al sisma e quindi verificare la loro reale capacità di dissipazione energetica. I più
importanti risultati delle prove dinamiche e delle simulazioni numeriche sono riportati in [2] e [3].
Anche in ambito internazionale sono in atto numerose prove sperimentali accompagnate da
simulazioni numeriche con lo scopo di riprodurre fedelmente il comportamento isteretico delle
connessioni chiodate legno acciaio e quindi la risposta dell’intera struttura sotto l’azione sismica. In
[4] viene descritto un modello numerico completo delle connessioni con il quale è possibile
simulare attraverso delle analisi non lineari la risposta al sisma degli edifici in legno.
MODELLO NUMERICO DELLE CONNESSIONI -
Gli edifici XLam sono realizzati mediante l’assemblaggio di pannelli in legno lamellare a strati
incrociati uniti tra loro attraverso specifici elementi di connessione. Per questo sistema costruttivo si
utilizzano normalmente i seguenti elementi di unione:
- angolari: impediscono lo scorrimento delle pareti
- holdown: impediscono il sollevamento delle pareti dal piano di fondazione
- viti: limitano gli spostamenti relativi tra i pannelli delle pareti

Fig.1 - Da sinistra, esempio di angolare, holdown e viti per il collegamento dei pannelli.
Le strutture in legno presentano un buon livello di duttilità e capacità dissipativa grazie al
contemporaneo fenomeno della plasticizzazione dell’acciaio nel connettore metallico e dello
schiacciamento localizzato del legno (rifollamento) per effetto dell’azione concentrata del
connettore.
Il diagramma forza scorrimento di una connessione realizzata con chiodi e sottoposta ad un carico
di tipo ciclico, presenta la tipica forma a fiocco (o a farfalla), in cui il corpo centrale si assottiglia a
mano a mano che si procede verso valori più alti del carico.
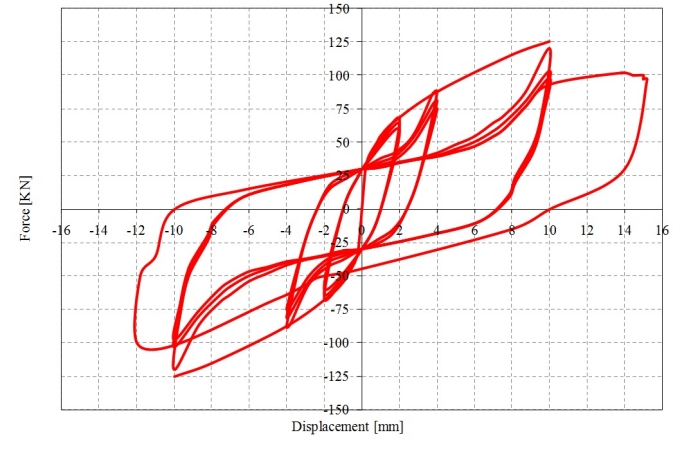
Fig.2 - Diagramma forza-spostamento tipico di un’unione chiodata
Il comportamento ciclico tipico di una connessione chiodata presenta i seguenti aspetti:
- curva di carico vergine diversa da quella dei successivi cicli di carico
- riduzione di rigidezza per i cicli di carico di ampiezza superiore
- riduzione di resistenza per i cicli di carico ripetuti di uguale ampiezza
- presenza di un limite di rottura
Una corretta progettazione della connessione assicura un comportamento duttile, con la minima
riduzione delle caratteristiche di resistenza e rigidezza, e un elevato valore della dissipazione
energetica. L’insieme di tali aspetti positivi si può sintetizzare con il termine “robustezza”.
Qualora si voglia realizzare un modello numerico capace di riprodurre in modo fedele il
comportamento isteretico della connessione, devono essere presi in considerazione tutti gli aspetti
sopra descritti. Solamente legami costitutivi complessi riescono a tenere conto contemporaneamente
di tali aspetti; un esempio di modello numerico capace di riprodurre in modo fedele il
comportamento isteretico della connessione è riportato in [4]. Tale approccio è utile per lo studio
del comportamento della singola connessione ma risulta oneroso nel caso in cui si voglia indagare
sul comportamento di un intero edifico nel quale è presente un elevato numero di elementi di
connessione differenti tra loro (angolari, holdown, giunti verticali).
Per descrivere la risposta al sisma, in ambito non lineare, di un intero edificio è infatti necessario
utilizzare un legame costitutivo delle connessioni semplificato senza compromettere la qualità dei
risultati. Ciò è possibile se si trascurano gli aspetti: di decadimento della resistenza della
connessione per cicli di carico ripetuti e di presenza del limite di rottura. La riduzione di rigidezza
della connessione non può invece essere trascurata in quanto è responsabile dell’aumento del
periodo proprio dell’edificio e la conseguente diminuzione della suscettibilità al sisma. Nonostante
le semplificazioni, deve essere mantenuta una corrispondenza tra la forma del ciclo isteretico della
simulazione numerica e quella sperimentale, in termini di forze e spostamenti massimi, nonché di
energia dissipata.
Nell’ambito del lavoro svolto, è stato possibile riprodurre il comportamento della connessione
mediante la combinazione di più molle, aventi legami costitutivi semplici di tipo elasto-plastico
incrudente, opportunamente combinati all’interno di un macroelemento complesso.
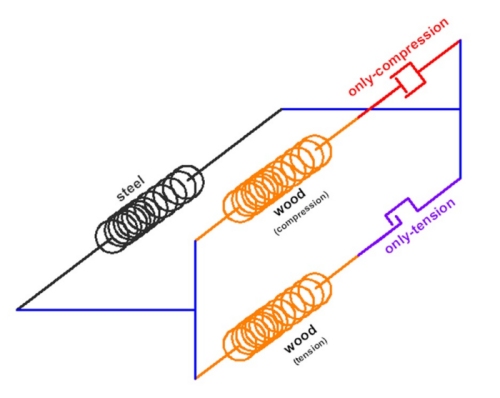
Fig.3 - Macroelemento di connessione
Come mostra la Fig.3 il macroelemento vede in parallelo una molla elastoplastica che fornisce il
contributo di rigidezza del gambo del connettore (steel) e una molla equivalente che rappresenta il
legno (wood). Quest’ultima è a sua volta un macroelemento costituito da due molle in parallelo, una
in serie con un elemento only-compression che lavora per accorciamenti della connessione e una in
serie con un elemento only-tension che lavora invece per allungamenti. Gli elementi plastici only-compression
e only-tension permettono di rappresentare l’effetto di ovalizzazione del foro e la
formazione del gioco all’interno della connessione. Il macroelemento descritto consente di
riprodurre la forma a fiocco del ciclo isteretico simmetrico, tipico degli angolari. Esso può essere
facilmente modificato per riprodurre i cicli asimmetrici tipici degli holdown. Quest’ultimi infatti,
per sforzi di compressione, presentano un’elevata rigidezza in quanto non si assiste al fenomeno del
rifollamento del legno nei punti di contatto con i chiodi bensì ad uno schiacciamento localizzato
della parete nella zona di contatto con il supporto (fondazione o solaio). Modificando
opportunamente il legame costitutivo della molla del legno, che lavora per soli sforzi di
compressione, è stato possibile riprodurre tale comportamento e più in generale quello di un
qualsiasi giunto che presenti un comportamento asimmetrico. I macroelementi così pensati possono
essere accoppiati per generare giunti che hanno comportamenti diversi nelle due direzioni x e y
come per esempio i giunti verticali tra le pareti per i quali il ciclo isteretico è simmetrico nelle
direzione verticale e asimmetrico per quella orizzontale. Le caratteristiche proprie di ogni singolo
componente del macroelemento vengono scelte in funzione del tipo di connessione e del numero di
chiodi impiegati. La taratura di ciascuna molla è stata basata sui risultati delle prove sperimentali e
sui valori di resistenza massima della connessione indicati dalle normative [5]
TARATURA DEL MODELLO E TEST DI VALIDAZIONE
Modellazione delle connessioni singole
La validazione del macroelemento descritto è stata effettuata facendo riferimento ai risultati delle
prove sperimentali condotte nell’ambito del progetto SOFIE. In particolare sono stati utilizzate le
curve carico spostamento, riportate in [3], relative alle prove cicliche realizzate sui giunti. Tali
curve consentono la taratura di tutti i parametri del macroelemento. In Fig.5 è riportata la
corrispondenza tra i valori di rigidezza delle molle del macroelemento e le rigidezze dei vari tratti
linearizzati della curva carico spostamento della connessione. In riferimento al ciclo isteretico
simmetrico dell’angolare:
- le rigidezze a e b delle molle legno corrispondono alla pendenza dei tratti elastici della curva
monotona della connessione
- le rigidezze c e d degli elementi only-tension e only-compression corrispondono alla
pendenza dei tratti plastici della curva monotona della connessione
- la molla steel presenta un legame elastoplastico: la rigidezza e del tratto elastico corrisponde
alla pendenza all’origine della curva di carico monotono della connessione, la forza Fo che
porta allo snervamento corrisponde all’intercetta della curva isteretica con l’asse delle
ordinate mentre la rigidezza del tratto incrudente f corrisponde alla pendenza del corpo
centrale del fiocco
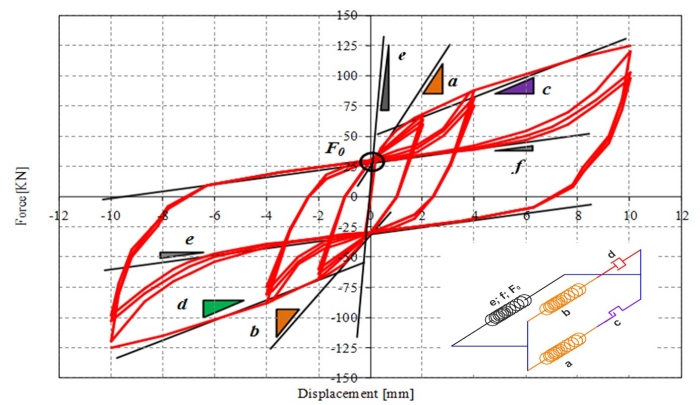
Fig.4 - Parametri per la taratura del macroelemento
Per gli elementi di connessione asimmetrici la taratura avviene con i medesimi criteri tenendo conto
delle differenze in termini di rigidezza nelle molle del legno che lavorano per gli accorciamenti
della connessione (b e d).
Una volta tarato il macroelemento è possibile riprodurre il ciclo isteretico tipico degli elementi di
connessione. In Fig.5 viene riportato un confronto tra i risultati delle prove cicliche complete
sperimentali condotte su angolari e holdown e le rispettive simulazioni numeriche.
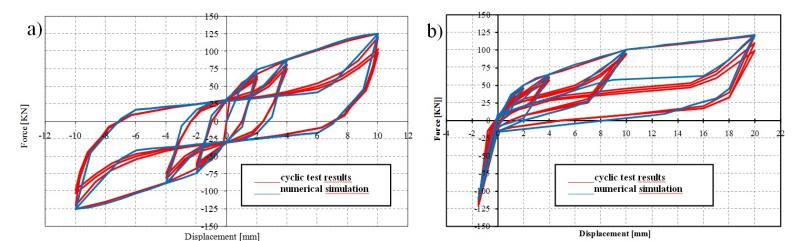
Fig.5 - Curva carico spostamento degli elementi di connessione a)angolari, b)holdown
Tali curve sono state ottenute con i valori delle rigidezze delle molle del macroelemento riportate in Table 1 -:
Table 1 - Valori delle rigidezze delle molle dei macroelementi

Si osserva che il macroelemento realizzato riproduce la tipica forma a fiocco e la riduzione di
rigidezza per i cicli di ampiezza maggiore ma non riesce, come dalle ipotesi di base, a riprodurre la
riduzione di resistenza della connessione e la presenza di un tratto discendente della curva di carico.
Ciò è dovuto all’impiego di elementi finiti standard, disponibili nella libreria del codice di calcolo
commerciale utilizzato che non consente di descrive un comportamento di tipo softening.
Simulazione di test su parete singola
Per verificare l’interazione tra pannello parete - giunti di base (angolari e holdown) e l’effetto del
carico verticale, si è simulata la prova ciclica completa nella configurazione 3b descritta in [1].
La modellazione della parete si basa sull’ipotesi che il comportamento non lineare della stessa sia
dovuto esclusivamente ai connettori (angolari e holdown) mentre il pannello XLam si mantiene
sempre in campo elastico. Per modellare la parete sono stati utilizzati i macroelementi
precedentemente costruiti per rappresentare il comportamento non lineare delle connessioni, mentre
il pannello XLam è stato realizzato con degli elementi Plate, di spessore pari a quello del pannello
(85mm), a comportamento elastico. Il pannello di legno ha un comportamento di tipo elastico
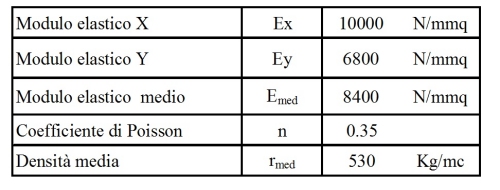
isotropo con un modulo di elasticità medio fra quelli secondo le due direzioni principali X e Y. Le
caratteristiche del pannello XLam sono specificate in Table 2 -:
Table 2 - Caratteristiche meccaniche del pannello XLam
Il carico verticale è stato applicato in modo distribuito. La prova ciclica è stata simulata assegnando
uno spostamento orizzontale imposto ai nodi posti sulla sommità della parete. La Fig.6 mostra il
modello utilizzato indicando la posizione degli holdovn e degli angolari.
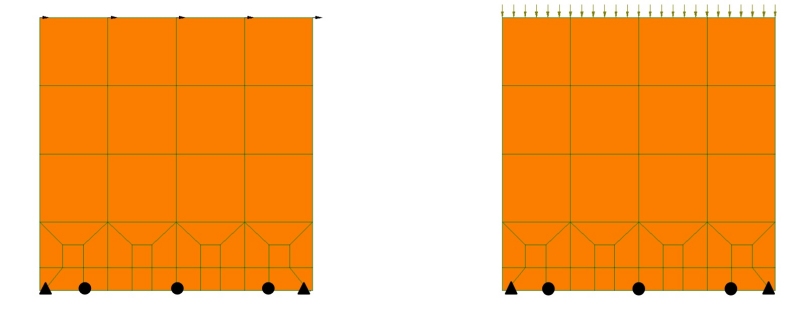
Fig.6 - Indicazione delle connessioni nel modello numerico della parete: holdown e angolari
La curva carico spostamento riportata in Fig.7 mostra la perfetta corrispondenza tra i risultati della
prova ciclica sperimentale e la simulazione numerica. sia in termini di forma del ciclo isteretico che
nei valori di forza e spostamento ad ogni ciclo. I valori della forza per ogni spostamento imposto in
sommità sono ottenuti come somma delle reazioni orizzontali alla base.
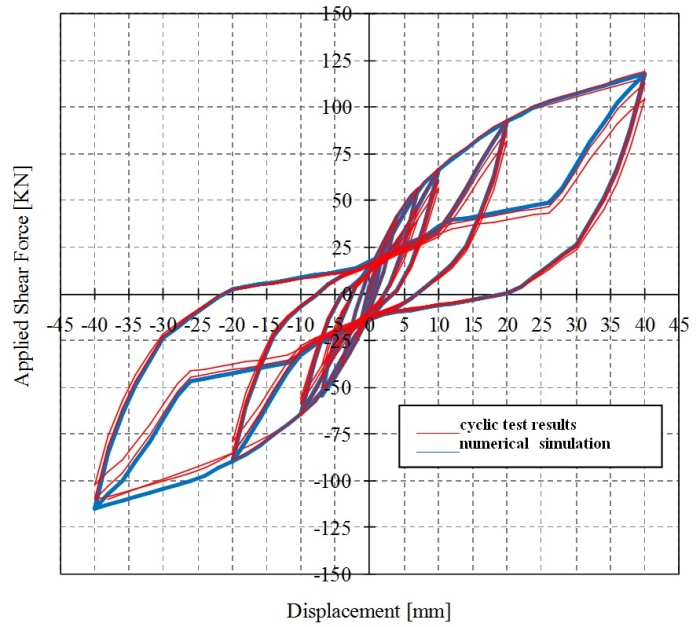
Fig.7 - Confronto tra i risultati della prova ciclica completa sperimentale e la simulazione
numerica.
La buona qualità della modellazione proposta è ribadita anche attraverso la valutazione dell’energia
dissipata, parametro fondamentale per caratterizzare il comportamento sismico di qualsiasi tipologia
costruttiva. In una prova ciclica è possibile calcolare il valore dello smorzamento viscoso
equivalente Veq, parametro adimensionale che esprime le proprietà di smorzamento isteretico
dell’elemento strutturale ed è definito in accordo con [1] come:
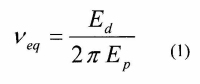
dove:
- Ed = energia dissipata in metà ciclo per effetto delle deformazioni plastiche
- Ep = energia potenziale disponibile (quella assorbita dal sistema)
I valori di energia che compaiono nella formula corrispondono alle aree tratteggiate in Fig.8.
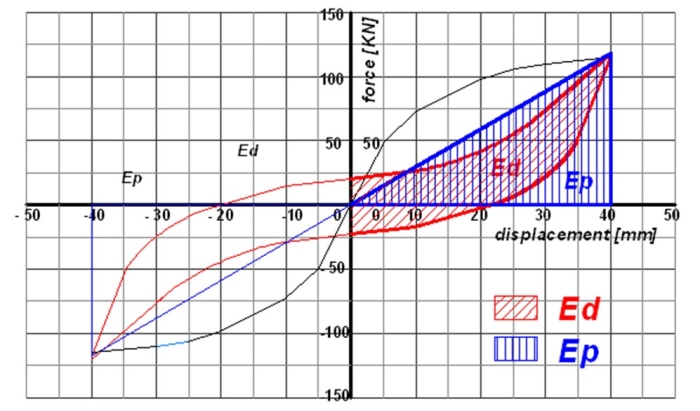
Fig.8 - Indicazione delle aree corrispondenti all’energia potenziale Ep e all’energia dissipata Ep
all’interno del ciclo isteretico della connessione
Il valore dello smorzamento viscoso equivalente ottenuto dalla simulazione numerica risulta pari a
12.85% valore di poco differente dal 13.10% ottenuto dalla prova sperimentale.
Simulazione di prova su tavola vibrante di edifici reali
I test di validazione sopra riportati non sono esaustivi per verificare la capacità da parte del
macroelemento di riprodurre il comportamento di un intero edifico sotto l’azione sismica. Pertanto
si è proceduto alla riproduzione numerica delle prove sperimentali descritte in Fig.2 dell’edificio a
tre piani testato su tavola vibrante, nella configurazione denominata C che presenta delle aperture
asimmetriche al piano terra.
Il modello numerico è stato realizzato in modo analogo a quanto visto per il singolo pannello parete:
- pareti realizzate con elementi plate, di caratteristiche analoghe a quelle del test precedente
(Table 1 -);
- giunti di connessione di base e interpiano, realizzati attraverso i macroelementi
precedentemente introdotti;
- giunti di connessione verticale, realizzati mediante l’accoppiamento di un macroelemento a
ciclo simmetrico per la direzione verticale e uno asimmetrico per quella orizzontale;
- solai di piano e copertura, realizzati con elementi Plate, analoghi alle pareti ma con spessore
pari a quello effettivo dell’elemento strutturale
- masse di piano applicate a livello dei solai
Il modello agli elementi finiti dell’edificio utilizzato nelle analisi è riportato nell’immagine che
segue:
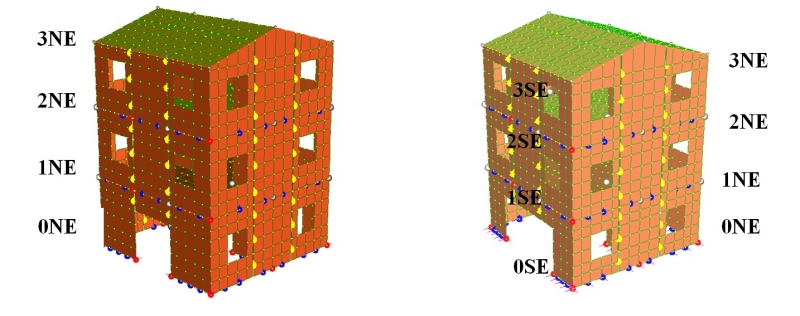
Fig.9 - Viste del modello dell’intero edificio con indicazione delle connessioni, masse di piano e
punti di controllo degli spostamenti utilizzati nei test sperimentali e nelle analisi.
L’edificio così modellato è stato sottoposto al sisma di Kobe (registrato il 16/01/1995 nella stazione
JMA con PGA=0.82g), applicato in un’unica direzione, parallelamente alle pareti aventi le aperture
di accesso al piano terra. L’equazione del moto sono state integrate con un passo temporale di 0.001
sec, adottando uno smorzamento viscoso del 2%, secondo il modello alla Rayleigh.
I risultati dell’analisi non lineare nel dominio del tempo, sotto l’input sismico di Kobe, hanno
confermato la capacità del modello numerico e dei macroelementi di connessione di riprodurre il
comportamento in ambito non lineare dell’intero edificio. A conferma di ciò, si riporta in Table 3 -
di confronto tra i risultati della prova sperimentale e della simulazione numerica in termini di
spostamenti massimi di piano e sollevamento degli holdown in corrispondenza dei punti di
controllo riportati in Fig.9.
Table 3 - Confronto tra i risultati della prove sperimentali e della simulazione numerica.

Lo scostamento tra i risultati della prova sperimentale e la simulazione numerica è sempre inferiore
al 5%, per ogni valore considerato. Il confronto, in termini di configurazione deformata, con i
risultati della simulazione numerica riportati in [3] sul medesimo edificio, conferma la capacità dei
macroelementi di connessione di poter essere utilizzati in modelli complessi per valutare la risposta
dell’edificio al sisma.
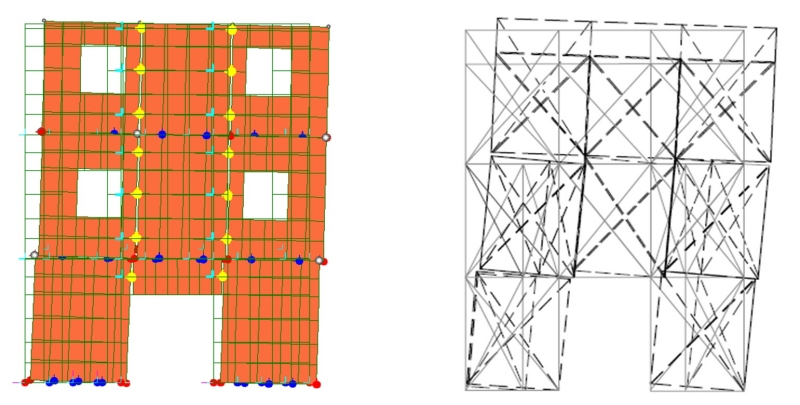
Fig.10 A sinistra configurazione deformata del presente modello; a destra, configurazione
deformata della simulazione numerica riportata in [3]
VALUTAZIONE DEL FATTORE ‘Q’
Una volta validato il modello numerico proposto, esso è stato utilizzato per sottoporre una generica
struttura ad un qualsivoglia evento sismico naturale o generato artificialmente, allo scopo di
verificarne la capacità dissipativa espressa attraverso il fattore di struttura ‘q’ che riassume il
comportamento post-elastico e la duttilità della costruzione.
La procedura adottata in [3] per determinare il fattore di struttura è costituita dai seguenti punti:
I. Costruzione di un modello agli elementi finiti dell’edificio in esame capace di riprodurre il
comportamento isteretico degli elementi di connessione presenti;
II. Definizione di una condizione ultima o di quasi collasso (‘near collapse’) dell’edificio la
quale può coincidere con lo spostamento ultimo di un elemento di connessione impiegato;
III. Valutazione dell’intensità del sisma che porta al raggiungimento della condizione “ultima”
attraverso una serie di analisi non lineari nel dominio del tempo con incremento graduale
della sua intensità;
IV. Determinazione del fattore di struttura corrispondente come rapporto tra l’accelerazione
nella condizione di quasi collasso e l’accelerazione utilizzata per il progetto in campo
elastico.
A rigore, questa strategia consente di verificare se il valore del fattore q indicato dalla normativa sia
corretto per la progettazione ma non di definirlo in modo esatto in quanto viene fissata a priori
l’intensità del sisma che porta allo snervamento. Tale accelerazione, in analogia con quella che
porta al collasso, dovrebbe essere determinata con una serie di analisi non lineari previa definizione
di un limite di snervamento. Non esiste però una definizione di snervamento, di un intero edificio,
universalmente riconosciuta pertanto nell’ approccio proposto in [3] si ipotizza che l’edificio
raggiunga lo snervamento per valori di accelerazione pari a quello di progetto e sia costante
indipendentemente dal contenuto in frequenza del sisma considerato. Diversamente il valore
dell’accelerazione che porta al raggiungimento della condizione di quasi collasso, essendo
determinato attraverso un’analisi non lineare, tiene conto del contenuto in frequenza del sisma e non
è costante ma variabile in funzione del periodo proprio dell’edificio in esame.
Qui si propone un approccio alternativo, per superare tale inconveniente che consiste nel definire il
fattore di struttura q come il rapporto tra il taglio alla base calcolato nell’ipotesi di risposta elastica
non dissipativa e nel caso di risposta dissipativa per il valore di intensità sismica di quasi collasso.
In questo modo i valori presenti nel rapporto sono coerenti in quanto provenienti ambedue da
un’analisi che riesce a tener conto del contenuto in frequenza del sisma in rapporto alle
caratteristiche dell’edificio. Di contro questa strategia presenta un onere computazionale maggiore
in quanto si devono eseguire due analisi dinamiche e estrapolare per ciascuna i valori del taglio alla
base dell’edifico.
Nell’ambito del lavoro svolto si è fatto riferimento ad ambedue le metodologie di calcolo del fattore
q. Per ottenere risultati significativi, si sono condotte le analisi su tre edifici test aventi periodi
fondamentali diversi, progettati in modo da resistere in campo elastico ad un sisma di massima
intensità per il territorio italiano (PGA=0,35g). Dei tre edifici studiati uno è quello testato su tavola
vibrante e descritto nel paragrafo precedente, mentre gli altri due presentano la medesima geometria
ma valori delle masse e delle caratteristiche delle connessioni differenti.
Il calcolo del fattore q è stato eseguito in riferimento a 5 differenti forzanti sismiche generate
artificialmente in modo da soddisfare il requisito di spettro compatibilità. Ciascun edificio test è
stato sottoposto, a partire dal valore dell’accelerazione di picco di 0.35g, ad un livello crescente
dell’intensità sismica fino al raggiungimento della condizione di collasso che, in accordo con [3],
coincide con un sollevamento di uno degli holdown alla base di 25.5mm. Per tale condizione ultima
è stato letta l’intensità del taglio alla base oltre che il valore dell’accelerazione di picco. Per il sisma
che porta al collasso l’edifico, è stata eseguita un’ulteriore analisi dinamica considerando un
comportamento non dissipativo delle connessioni e valutando per questa condizione l’intensità del
taglio alla base. Applicando i due metodi sopra descritti è stato definito il fattore q per ciascuno dei
tre edifici test e per ciascuna delle 5 forzanti sismiche considerate. I risultati sono riassunti in Table
4 - e nel grafico riportato in Fig.10.
Table 4 - Valori del fattore q per ciascuno dei casi esaminati.
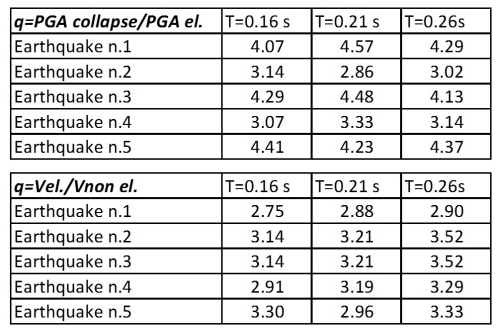
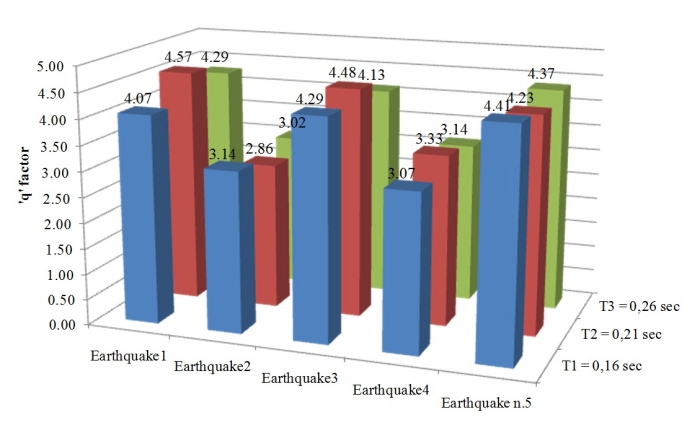
Fig.11-a
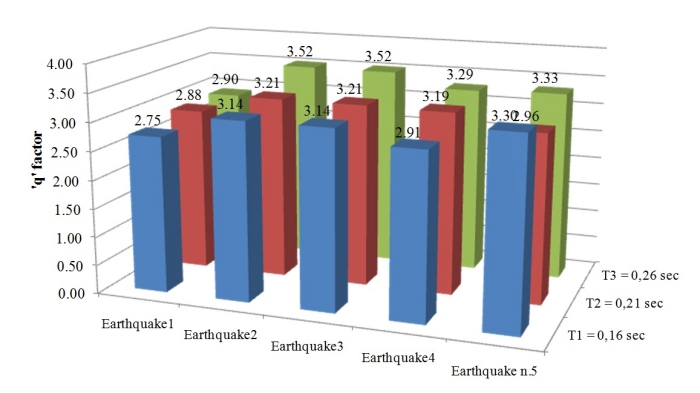
Fig.11-b
Fig.11 - Valori del fattore q: a) calcolati con l’approccio basato sulle PGA, b) calcolati con
l’approccio basato sui tagli alla base
Dai grafici si può osservare che i valori del fattore q calcolati come rapporti dei tagli alla base,
presentano una minore variabilità rispetto a quelli definiti dal rapporto delle accelerazioni, a
conferma dei limiti che quest’ultimo approccio presenta nella definizione dell’accelerazione di
a)
b)
picco che porta allo snervamento l’edificio. Va osservato che l’approccio basato sui tagli alla base
presenta valori tendenzialmente inferiori del fattore ‘q’, in ogni caso i risultati si assestano sul
valore q=3 indipendentemente dal contenuto in frequenza della forzante sismica e dal periodo
dell’edificio.
CONCLUSIONI
Il lavoro svolto conferma la possibilità di riprodurre la risposta al sisma in ambito non lineare delle
strutture XLam utilizzando anche codici di calcolo commerciali attraverso macroelementi specifici
necessari per rappresentare gli elementi di connessione. La corretta taratura di tali macroelementi,
sulla base dei test sperimentali, costituisce un requisito fondamentale per riprodurre il
comportamento della singola connessione e più in generale di un intero edificio.
Le simulazioni numeriche effettuate su edifici test diversi per massa e rigidezza, hanno dimostrato
che questa tipologia costruttiva possiede una buona capacità di dissipazione energetica grazie alla
presenza dei giunti metallici che garantiscono un buon livello di duttilità globale.
La capacità dissipativa, sintetizzata attraverso il fattore ‘q’, è stata valutata seguendo due approcci
diversi e per varie forzanti sismiche. I risultati ottenuti confermano che l’adozione di un fattore di
struttura ‘q’ pari a 3 è appropriata per la progettazione di questa tipologia costruttiva.
RINGRAZIAMENTI
Si ringrazia la HSH s.r.l. di Padova per la fornitura del software ad elementi finiti “Straus7”
utilizzato per tutte le analisi statiche e dinamiche con non linearità per materiale condotte
nell’ambito del presente lavoro.
REFERENCES
[1] CECCOTTI, A. LAURIOLA, M. P. PINNA, M. SANDHAAS, C. : SOFIE Project – Cyclic Tests on
Cross-Laminated Wooden Panels, Proceedings WCTE, Portland, USA, 2006
[2] CECCOTTI, A. FOLLESA, M. LAURIOLA, M. P.: La sperimentazione sismica sulle costruzioni di
legno: attualità e prospettive, Seminario CIAS, Cipro, 2007
[3] CECCOTTI, A. : New Technologies for Construction of Medium- Rise Buildings in Seismic Regions: The
XLAM Case, Structural Engineering International, Volume 18, Number 2, May 2008, pp. 156-165
[4] FOLZ, A. ASCE, M. FILIATRAULT, A. : Seismic Analysis of Woodframe Structures: Model Formulation,
ASCE/0733-9445, 2004
[5] EN 1995-1-1:2005. Eurocode 5 – Design of Timber Structure – Part 1-1: General – Common Rules and
Rules for Buildings
|
INTRODUZIONE -
Il sistema costruttivo XLam sta avendo una larga diffusione grazie alle sue ottime caratteristiche e
prestazioni. La sostenibilità e la convenienza dei moderni edifici in legno è legata sempre più al
fatto che essi sono integrati con dispositivi e soluzioni costruttive finalizzate al basso consumo
energetico in fase di gestione dell’edificio; ciò rende questa tipologia competitiva, efficiente e
sicura rispetto ad altre tipologie più classiche.
Dal punto di vista sismico gli edifici XLam manifestano un buon comportamento grazie alla loro
leggerezza e ad una buona capacità di dissipazione energetica. Le forze indotte dal sisma nella
struttura risultano infatti proporzionali alla massa ed inversamente proporzionali alla capacità di
dissipare energia. Il legno presenta un rapporto resistenza/peso molto vantaggioso se paragonato a
quello del calcestruzzo con il vantaggio che resiste anche a sforzi di trazione.
Nella pratica costruttiva i vari elementi lignei che costituiscono la struttura portante degli edifici
XLam vengono assemblati mediante connessioni di tipo metallico. Tali elementi di connessione, se
progettati in modo corretto, manifestano un comportamento duttile che va a conferire al sistema
“legno + connessione” un’ottima resistenza e robustezza alle azioni cicliche e quindi al sisma.
Nonostante questo sistema costruttivo sia diffuso nella pratica comune, nessuna indicazione
costruttiva o di calcolo è contenuta all’interno delle normative nazionali ed internazionali.
Indagini e ricerche, allo scopo di ottenere dati certi che possano costituire un valido supporto per
l’inserimento del sistema nelle prescrizioni normative, sono in corso soprattutto per quanto riguarda
lo studio della risposta all’azione sismica. Il più importante progetto di ricerca in Italia in atto è il
PROGETTO SOFIE finanziato dalla provincia autonoma di Trento e coordinato dal CNR-IVALSA.
Tale progetto si compone di prove sperimentali (monotone e cicliche) sui singoli elementi di
connessione e pannelli pareti. I risultati di tali prove sperimentali sono riportati in [1]. Significativi
sono i test dinamici condotti su edifici multipiano in XLam in scala reale su tavola vibrante. Tali
test sono stati accompagnati da simulazioni numeriche in ambito non lineare allo scopo di simulare
la loro risposta al sisma e quindi verificare la loro reale capacità di dissipazione energetica. I più
importanti risultati delle prove dinamiche e delle simulazioni numeriche sono riportati in [2] e [3].
Anche in ambito internazionale sono in atto numerose prove sperimentali accompagnate da
simulazioni numeriche con lo scopo di riprodurre fedelmente il comportamento isteretico delle
connessioni chiodate legno acciaio e quindi la risposta dell’intera struttura sotto l’azione sismica. In
[4] viene descritto un modello numerico completo delle connessioni con il quale è possibile
simulare attraverso delle analisi non lineari la risposta al sisma degli edifici in legno.  Fig.1 - Da sinistra, esempio di angolare, holdown e viti per il collegamento dei pannelli. Le strutture in legno presentano un buon livello di duttilità e capacità dissipativa grazie al contemporaneo fenomeno della plasticizzazione dell’acciaio nel connettore metallico e dello schiacciamento localizzato del legno (rifollamento) per effetto dell’azione concentrata del connettore. Il diagramma forza scorrimento di una connessione realizzata con chiodi e sottoposta ad un carico di tipo ciclico, presenta la tipica forma a fiocco (o a farfalla), in cui il corpo centrale si assottiglia a mano a mano che si procede verso valori più alti del carico.  Fig.2 - Diagramma forza-spostamento tipico di un’unione chiodata Il comportamento ciclico tipico di una connessione chiodata presenta i seguenti aspetti: - curva di carico vergine diversa da quella dei successivi cicli di carico - riduzione di rigidezza per i cicli di carico di ampiezza superiore - riduzione di resistenza per i cicli di carico ripetuti di uguale ampiezza - presenza di un limite di rottura Una corretta progettazione della connessione assicura un comportamento duttile, con la minima riduzione delle caratteristiche di resistenza e rigidezza, e un elevato valore della dissipazione energetica. L’insieme di tali aspetti positivi si può sintetizzare con il termine “robustezza”. Qualora si voglia realizzare un modello numerico capace di riprodurre in modo fedele il comportamento isteretico della connessione, devono essere presi in considerazione tutti gli aspetti sopra descritti. Solamente legami costitutivi complessi riescono a tenere conto contemporaneamente di tali aspetti; un esempio di modello numerico capace di riprodurre in modo fedele il comportamento isteretico della connessione è riportato in [4]. Tale approccio è utile per lo studio del comportamento della singola connessione ma risulta oneroso nel caso in cui si voglia indagare sul comportamento di un intero edifico nel quale è presente un elevato numero di elementi di connessione differenti tra loro (angolari, holdown, giunti verticali). Per descrivere la risposta al sisma, in ambito non lineare, di un intero edificio è infatti necessario utilizzare un legame costitutivo delle connessioni semplificato senza compromettere la qualità dei risultati. Ciò è possibile se si trascurano gli aspetti: di decadimento della resistenza della connessione per cicli di carico ripetuti e di presenza del limite di rottura. La riduzione di rigidezza della connessione non può invece essere trascurata in quanto è responsabile dell’aumento del periodo proprio dell’edificio e la conseguente diminuzione della suscettibilità al sisma. Nonostante le semplificazioni, deve essere mantenuta una corrispondenza tra la forma del ciclo isteretico della simulazione numerica e quella sperimentale, in termini di forze e spostamenti massimi, nonché di energia dissipata. Nell’ambito del lavoro svolto, è stato possibile riprodurre il comportamento della connessione mediante la combinazione di più molle, aventi legami costitutivi semplici di tipo elasto-plastico incrudente, opportunamente combinati all’interno di un macroelemento complesso.  Fig.3 - Macroelemento di connessione Come mostra la Fig.3 il macroelemento vede in parallelo una molla elastoplastica che fornisce il contributo di rigidezza del gambo del connettore (steel) e una molla equivalente che rappresenta il legno (wood). Quest’ultima è a sua volta un macroelemento costituito da due molle in parallelo, una in serie con un elemento only-compression che lavora per accorciamenti della connessione e una in serie con un elemento only-tension che lavora invece per allungamenti. Gli elementi plastici only-compression e only-tension permettono di rappresentare l’effetto di ovalizzazione del foro e la formazione del gioco all’interno della connessione. Il macroelemento descritto consente di riprodurre la forma a fiocco del ciclo isteretico simmetrico, tipico degli angolari. Esso può essere facilmente modificato per riprodurre i cicli asimmetrici tipici degli holdown. Quest’ultimi infatti, per sforzi di compressione, presentano un’elevata rigidezza in quanto non si assiste al fenomeno del rifollamento del legno nei punti di contatto con i chiodi bensì ad uno schiacciamento localizzato della parete nella zona di contatto con il supporto (fondazione o solaio). Modificando opportunamente il legame costitutivo della molla del legno, che lavora per soli sforzi di compressione, è stato possibile riprodurre tale comportamento e più in generale quello di un qualsiasi giunto che presenti un comportamento asimmetrico. I macroelementi così pensati possono essere accoppiati per generare giunti che hanno comportamenti diversi nelle due direzioni x e y come per esempio i giunti verticali tra le pareti per i quali il ciclo isteretico è simmetrico nelle direzione verticale e asimmetrico per quella orizzontale. Le caratteristiche proprie di ogni singolo componente del macroelemento vengono scelte in funzione del tipo di connessione e del numero di chiodi impiegati. La taratura di ciascuna molla è stata basata sui risultati delle prove sperimentali e sui valori di resistenza massima della connessione indicati dalle normative [5] TARATURA DEL MODELLO E TEST DI VALIDAZIONE Modellazione delle connessioni singole La validazione del macroelemento descritto è stata effettuata facendo riferimento ai risultati delle prove sperimentali condotte nell’ambito del progetto SOFIE. In particolare sono stati utilizzate le curve carico spostamento, riportate in [3], relative alle prove cicliche realizzate sui giunti. Tali curve consentono la taratura di tutti i parametri del macroelemento. In Fig.5 è riportata la corrispondenza tra i valori di rigidezza delle molle del macroelemento e le rigidezze dei vari tratti linearizzati della curva carico spostamento della connessione. In riferimento al ciclo isteretico simmetrico dell’angolare: - le rigidezze a e b delle molle legno corrispondono alla pendenza dei tratti elastici della curva monotona della connessione - le rigidezze c e d degli elementi only-tension e only-compression corrispondono alla pendenza dei tratti plastici della curva monotona della connessione - la molla steel presenta un legame elastoplastico: la rigidezza e del tratto elastico corrisponde alla pendenza all’origine della curva di carico monotono della connessione, la forza Fo che porta allo snervamento corrisponde all’intercetta della curva isteretica con l’asse delle ordinate mentre la rigidezza del tratto incrudente f corrisponde alla pendenza del corpo centrale del fiocco  Fig.4 - Parametri per la taratura del macroelemento Per gli elementi di connessione asimmetrici la taratura avviene con i medesimi criteri tenendo conto delle differenze in termini di rigidezza nelle molle del legno che lavorano per gli accorciamenti della connessione (b e d). Una volta tarato il macroelemento è possibile riprodurre il ciclo isteretico tipico degli elementi di connessione. In Fig.5 viene riportato un confronto tra i risultati delle prove cicliche complete sperimentali condotte su angolari e holdown e le rispettive simulazioni numeriche.  Fig.5 - Curva carico spostamento degli elementi di connessione a)angolari, b)holdown Tali curve sono state ottenute con i valori delle rigidezze delle molle del macroelemento riportate in Table 1 -:  Si osserva che il macroelemento realizzato riproduce la tipica forma a fiocco e la riduzione di rigidezza per i cicli di ampiezza maggiore ma non riesce, come dalle ipotesi di base, a riprodurre la riduzione di resistenza della connessione e la presenza di un tratto discendente della curva di carico. Ciò è dovuto all’impiego di elementi finiti standard, disponibili nella libreria del codice di calcolo commerciale utilizzato che non consente di descrive un comportamento di tipo softening. Simulazione di test su parete singola Per verificare l’interazione tra pannello parete - giunti di base (angolari e holdown) e l’effetto del carico verticale, si è simulata la prova ciclica completa nella configurazione 3b descritta in [1]. La modellazione della parete si basa sull’ipotesi che il comportamento non lineare della stessa sia dovuto esclusivamente ai connettori (angolari e holdown) mentre il pannello XLam si mantiene sempre in campo elastico. Per modellare la parete sono stati utilizzati i macroelementi precedentemente costruiti per rappresentare il comportamento non lineare delle connessioni, mentre il pannello XLam è stato realizzato con degli elementi Plate, di spessore pari a quello del pannello (85mm), a comportamento elastico. Il pannello di legno ha un comportamento di tipo elastico isotropo con un modulo di elasticità medio fra quelli secondo le due direzioni principali X e Y. Le caratteristiche del pannello XLam sono specificate in Table 2 -:  Il carico verticale è stato applicato in modo distribuito. La prova ciclica è stata simulata assegnando uno spostamento orizzontale imposto ai nodi posti sulla sommità della parete. La Fig.6 mostra il modello utilizzato indicando la posizione degli holdovn e degli angolari.  Fig.6 - Indicazione delle connessioni nel modello numerico della parete: holdown e angolari La curva carico spostamento riportata in Fig.7 mostra la perfetta corrispondenza tra i risultati della prova ciclica sperimentale e la simulazione numerica. sia in termini di forma del ciclo isteretico che nei valori di forza e spostamento ad ogni ciclo. I valori della forza per ogni spostamento imposto in sommità sono ottenuti come somma delle reazioni orizzontali alla base.  Fig.7 - Confronto tra i risultati della prova ciclica completa sperimentale e la simulazione numerica. La buona qualità della modellazione proposta è ribadita anche attraverso la valutazione dell’energia dissipata, parametro fondamentale per caratterizzare il comportamento sismico di qualsiasi tipologia costruttiva. In una prova ciclica è possibile calcolare il valore dello smorzamento viscoso equivalente Veq, parametro adimensionale che esprime le proprietà di smorzamento isteretico dell’elemento strutturale ed è definito in accordo con [1] come: 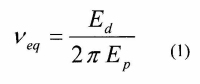 dove: - Ed = energia dissipata in metà ciclo per effetto delle deformazioni plastiche - Ep = energia potenziale disponibile (quella assorbita dal sistema) I valori di energia che compaiono nella formula corrispondono alle aree tratteggiate in Fig.8.  Fig.8 - Indicazione delle aree corrispondenti all’energia potenziale Ep e all’energia dissipata Ep all’interno del ciclo isteretico della connessione Il valore dello smorzamento viscoso equivalente ottenuto dalla simulazione numerica risulta pari a 12.85% valore di poco differente dal 13.10% ottenuto dalla prova sperimentale. Simulazione di prova su tavola vibrante di edifici reali I test di validazione sopra riportati non sono esaustivi per verificare la capacità da parte del macroelemento di riprodurre il comportamento di un intero edifico sotto l’azione sismica. Pertanto si è proceduto alla riproduzione numerica delle prove sperimentali descritte in Fig.2 dell’edificio a tre piani testato su tavola vibrante, nella configurazione denominata C che presenta delle aperture asimmetriche al piano terra. Il modello numerico è stato realizzato in modo analogo a quanto visto per il singolo pannello parete: - pareti realizzate con elementi plate, di caratteristiche analoghe a quelle del test precedente (Table 1 -); - giunti di connessione di base e interpiano, realizzati attraverso i macroelementi precedentemente introdotti; - giunti di connessione verticale, realizzati mediante l’accoppiamento di un macroelemento a ciclo simmetrico per la direzione verticale e uno asimmetrico per quella orizzontale; - solai di piano e copertura, realizzati con elementi Plate, analoghi alle pareti ma con spessore pari a quello effettivo dell’elemento strutturale - masse di piano applicate a livello dei solai Il modello agli elementi finiti dell’edificio utilizzato nelle analisi è riportato nell’immagine che segue:  Fig.9 - Viste del modello dell’intero edificio con indicazione delle connessioni, masse di piano e punti di controllo degli spostamenti utilizzati nei test sperimentali e nelle analisi. L’edificio così modellato è stato sottoposto al sisma di Kobe (registrato il 16/01/1995 nella stazione JMA con PGA=0.82g), applicato in un’unica direzione, parallelamente alle pareti aventi le aperture di accesso al piano terra. L’equazione del moto sono state integrate con un passo temporale di 0.001 sec, adottando uno smorzamento viscoso del 2%, secondo il modello alla Rayleigh. I risultati dell’analisi non lineare nel dominio del tempo, sotto l’input sismico di Kobe, hanno confermato la capacità del modello numerico e dei macroelementi di connessione di riprodurre il comportamento in ambito non lineare dell’intero edificio. A conferma di ciò, si riporta in Table 3 - di confronto tra i risultati della prova sperimentale e della simulazione numerica in termini di spostamenti massimi di piano e sollevamento degli holdown in corrispondenza dei punti di controllo riportati in Fig.9.  Lo scostamento tra i risultati della prova sperimentale e la simulazione numerica è sempre inferiore al 5%, per ogni valore considerato. Il confronto, in termini di configurazione deformata, con i risultati della simulazione numerica riportati in [3] sul medesimo edificio, conferma la capacità dei macroelementi di connessione di poter essere utilizzati in modelli complessi per valutare la risposta dell’edificio al sisma.  Fig.10 A sinistra configurazione deformata del presente modello; a destra, configurazione deformata della simulazione numerica riportata in [3] VALUTAZIONE DEL FATTORE ‘Q’ Una volta validato il modello numerico proposto, esso è stato utilizzato per sottoporre una generica struttura ad un qualsivoglia evento sismico naturale o generato artificialmente, allo scopo di verificarne la capacità dissipativa espressa attraverso il fattore di struttura ‘q’ che riassume il comportamento post-elastico e la duttilità della costruzione. La procedura adottata in [3] per determinare il fattore di struttura è costituita dai seguenti punti: I. Costruzione di un modello agli elementi finiti dell’edificio in esame capace di riprodurre il comportamento isteretico degli elementi di connessione presenti; II. Definizione di una condizione ultima o di quasi collasso (‘near collapse’) dell’edificio la quale può coincidere con lo spostamento ultimo di un elemento di connessione impiegato; III. Valutazione dell’intensità del sisma che porta al raggiungimento della condizione “ultima” attraverso una serie di analisi non lineari nel dominio del tempo con incremento graduale della sua intensità; IV. Determinazione del fattore di struttura corrispondente come rapporto tra l’accelerazione nella condizione di quasi collasso e l’accelerazione utilizzata per il progetto in campo elastico. A rigore, questa strategia consente di verificare se il valore del fattore q indicato dalla normativa sia corretto per la progettazione ma non di definirlo in modo esatto in quanto viene fissata a priori l’intensità del sisma che porta allo snervamento. Tale accelerazione, in analogia con quella che porta al collasso, dovrebbe essere determinata con una serie di analisi non lineari previa definizione di un limite di snervamento. Non esiste però una definizione di snervamento, di un intero edificio, universalmente riconosciuta pertanto nell’ approccio proposto in [3] si ipotizza che l’edificio raggiunga lo snervamento per valori di accelerazione pari a quello di progetto e sia costante indipendentemente dal contenuto in frequenza del sisma considerato. Diversamente il valore dell’accelerazione che porta al raggiungimento della condizione di quasi collasso, essendo determinato attraverso un’analisi non lineare, tiene conto del contenuto in frequenza del sisma e non è costante ma variabile in funzione del periodo proprio dell’edificio in esame. Qui si propone un approccio alternativo, per superare tale inconveniente che consiste nel definire il fattore di struttura q come il rapporto tra il taglio alla base calcolato nell’ipotesi di risposta elastica non dissipativa e nel caso di risposta dissipativa per il valore di intensità sismica di quasi collasso. In questo modo i valori presenti nel rapporto sono coerenti in quanto provenienti ambedue da un’analisi che riesce a tener conto del contenuto in frequenza del sisma in rapporto alle caratteristiche dell’edificio. Di contro questa strategia presenta un onere computazionale maggiore in quanto si devono eseguire due analisi dinamiche e estrapolare per ciascuna i valori del taglio alla base dell’edifico. Nell’ambito del lavoro svolto si è fatto riferimento ad ambedue le metodologie di calcolo del fattore q. Per ottenere risultati significativi, si sono condotte le analisi su tre edifici test aventi periodi fondamentali diversi, progettati in modo da resistere in campo elastico ad un sisma di massima intensità per il territorio italiano (PGA=0,35g). Dei tre edifici studiati uno è quello testato su tavola vibrante e descritto nel paragrafo precedente, mentre gli altri due presentano la medesima geometria ma valori delle masse e delle caratteristiche delle connessioni differenti. Il calcolo del fattore q è stato eseguito in riferimento a 5 differenti forzanti sismiche generate artificialmente in modo da soddisfare il requisito di spettro compatibilità. Ciascun edificio test è stato sottoposto, a partire dal valore dell’accelerazione di picco di 0.35g, ad un livello crescente dell’intensità sismica fino al raggiungimento della condizione di collasso che, in accordo con [3], coincide con un sollevamento di uno degli holdown alla base di 25.5mm. Per tale condizione ultima è stato letta l’intensità del taglio alla base oltre che il valore dell’accelerazione di picco. Per il sisma che porta al collasso l’edifico, è stata eseguita un’ulteriore analisi dinamica considerando un comportamento non dissipativo delle connessioni e valutando per questa condizione l’intensità del taglio alla base. Applicando i due metodi sopra descritti è stato definito il fattore q per ciascuno dei tre edifici test e per ciascuna delle 5 forzanti sismiche considerate. I risultati sono riassunti in Table 4 - e nel grafico riportato in Fig.10.   Fig.11-a  Fig.11-b Fig.11 - Valori del fattore q: a) calcolati con l’approccio basato sulle PGA, b) calcolati con l’approccio basato sui tagli alla base Dai grafici si può osservare che i valori del fattore q calcolati come rapporti dei tagli alla base, presentano una minore variabilità rispetto a quelli definiti dal rapporto delle accelerazioni, a conferma dei limiti che quest’ultimo approccio presenta nella definizione dell’accelerazione di a) b) picco che porta allo snervamento l’edificio. Va osservato che l’approccio basato sui tagli alla base presenta valori tendenzialmente inferiori del fattore ‘q’, in ogni caso i risultati si assestano sul valore q=3 indipendentemente dal contenuto in frequenza della forzante sismica e dal periodo dell’edificio. CONCLUSIONI Il lavoro svolto conferma la possibilità di riprodurre la risposta al sisma in ambito non lineare delle strutture XLam utilizzando anche codici di calcolo commerciali attraverso macroelementi specifici necessari per rappresentare gli elementi di connessione. La corretta taratura di tali macroelementi, sulla base dei test sperimentali, costituisce un requisito fondamentale per riprodurre il comportamento della singola connessione e più in generale di un intero edificio. Le simulazioni numeriche effettuate su edifici test diversi per massa e rigidezza, hanno dimostrato che questa tipologia costruttiva possiede una buona capacità di dissipazione energetica grazie alla presenza dei giunti metallici che garantiscono un buon livello di duttilità globale. La capacità dissipativa, sintetizzata attraverso il fattore ‘q’, è stata valutata seguendo due approcci diversi e per varie forzanti sismiche. I risultati ottenuti confermano che l’adozione di un fattore di struttura ‘q’ pari a 3 è appropriata per la progettazione di questa tipologia costruttiva. RINGRAZIAMENTI Si ringrazia la HSH s.r.l. di Padova per la fornitura del software ad elementi finiti “Straus7” utilizzato per tutte le analisi statiche e dinamiche con non linearità per materiale condotte nell’ambito del presente lavoro. REFERENCES [1] CECCOTTI, A. LAURIOLA, M. P. PINNA, M. SANDHAAS, C. : SOFIE Project – Cyclic Tests on Cross-Laminated Wooden Panels, Proceedings WCTE, Portland, USA, 2006 [2] CECCOTTI, A. FOLLESA, M. LAURIOLA, M. P.: La sperimentazione sismica sulle costruzioni di legno: attualità e prospettive, Seminario CIAS, Cipro, 2007 [3] CECCOTTI, A. : New Technologies for Construction of Medium- Rise Buildings in Seismic Regions: The XLAM Case, Structural Engineering International, Volume 18, Number 2, May 2008, pp. 156-165 [4] FOLZ, A. ASCE, M. FILIATRAULT, A. : Seismic Analysis of Woodframe Structures: Model Formulation, ASCE/0733-9445, 2004 [5] EN 1995-1-1:2005. Eurocode 5 – Design of Timber Structure – Part 1-1: General – Common Rules and Rules for Buildings |
Per inviare un messaggio: hsh@iperv.it