UNIVERSITÀ DEGLI STUDI DI PADOVA

 

 

 

 

 

 

 

 

 

 


FACOLTÀ DI INGEGNERIA

Corso di Laurea in Ingegneria Civile

Dipartimento di Costruzioni e Trasporti

 

 

 

 

TESI DI LAUREA

 

 

 

Procedure numeriche non lineari

per analisi sismiche

 

 

 

 

 

Relatore:  Ch.mo Prof. Lamberto Briseghella

Correlatore:  Ing. Stefano Secchi

Tesista:  Federico Tosi

 

 

 

 

 

 

 

 

 

Il lavoro svolto in questa tesi consiste nello studio dei metodi di analisi proposti dalla nuova Ordinanza 3274 del 08/05/2003[1]:

L’applicazione riguarda un telaio in acciaio multipiano regolare dimensionato secondo diversi metodi di progettazione per la realizzazione di edifici resistenti in zona sismica.

L’obiettivo è quello di valutare le procedure proposte dall’Ordinanza e determinare le capacità di resistenza e di duttilità di strutture progettate secondo normativa.

Il telaio preso in considerazione è il seguente:

 

 

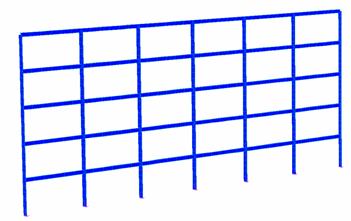
                                Acciaio:                         Fe430

                                Numero di piani:           5

                                Altezza di interpiano:    3.2 m

                                Numero campate:          6

                                Luce campate:               6.5 m

                                Travi:                             IPE 330

                                Carico permanente:       15 kN/m

                                Carico accidentale:        10 kN/m

 

 

 

                                                    

          

Fig.1 Telaio in acciaio

 

Analisi statica non lineare

 

Il metodo proposto dall’Ordinanza consiste nell’applicare oltre ai carichi verticali alcune distribuzioni di forze orizzontali crescenti sulla struttura.

Con il programma di calcolo Straus7 si determina la curva Forza-Spostamento con le seguenti distribuzioni di forze orizzontali:

  1. “Uniforme”: forze proporzionali alle masse
  2. “Modale”: forze proporzionali al prodotto tra le masse e la deformata individuata dal primo modo di vibrare.

Lo spostamento preso in considerazione è usualmente la sommità del telaio.

 

 

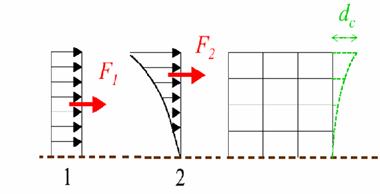
Fig. 2 Distribuzioni di forze

 

Si studia la risposta del telaio, espressa mediante lo spostamento di sommità, in campo plastico[4].

Tale risposta deve essere ottenuta mediante un’analisi non lineare che tenga conto degli effetti della non linearità geometrica e della  non linearità del materiale. La non linearità del materiale viene introdotta nel programma di calcolo mediante i diagrammi Momento-Curvatura.

Tale diagramma richiede il valore del momento di snervamento Me, oltre il quale la sezione inizia a plasticizzarsi,  e la rispettiva curvatura. E’ richiesto anche il calcolo del momento di plasticizzazione ultimo Mp a cui è associato un valore della curvatura limite che corrisponde alla prima fibra della sezione che raggiunge la deformazione massima consentibile.

Al crescere del carico, il momento elastico Me si raggiunge nell’istante in cui la tensione nelle fibre estreme raggiunge il valore dello snervamento del materiale:   , con We = modulo di resistenza elastico. Se si incrementa ulteriormente il momento flettente, la plasticizzazione delle fibre estreme si estende verso il centro e l’andamento delle tensioni si modifica fino a diventare bi-rettangolare. Alla piena plasticizzazione si ha la formazione della cerniera plastica caratterizzata dal massimo momento che la sezione può sopportare:, con Wp = modulo di resistenza plastico della sezione.

 

 

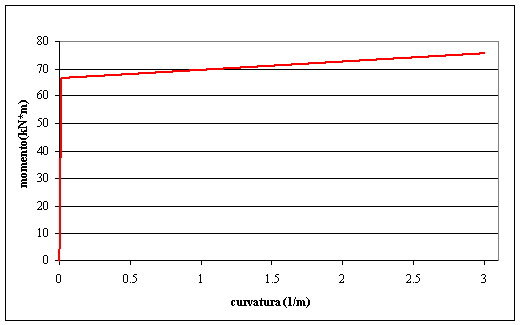
Fig. 3 Momemto-curvatura HEB160

 

In genere una sezione è soggetta ad azioni combinate di flessione, taglio e sforzo normale per cui il momento ultimo non può raggiungere il valore del momento plastico a causa della contemporanea presenza di queste sollecitazioni che riducono la capacità plastica flessionale della sezione[3]. L’influenza delle componente assiale può essere introdotta mediante un opportuno coefficiente che ha lo scopo di diminuire i valori del momento plastico ultimo.

In un’analisi non lineare è necessario considerare la diminuzione della capacità plastica di una sezione dovuta alla sollecitazione assiale.

Dato che la forza assiale aumenta all’aumentare dell’incremento di carico per avere un risultato corretto la procedura da svolgere è quella di modificare il diagramma momento-curvatura ad ogni iterazione dell’analisi non lineare, introducendo per ogni elemento il valore dello sforzo assiale calcolato nell’iterazione precedente.

Di seguito si riporta la curva di capacità ottenuta dall’analisi statica non lineare per le due distribuzioni di forze orizzontali.

 

 

 

 

 

 

 

 

 

 

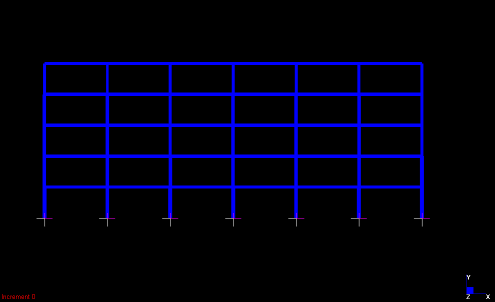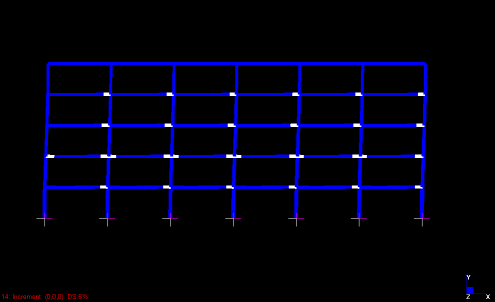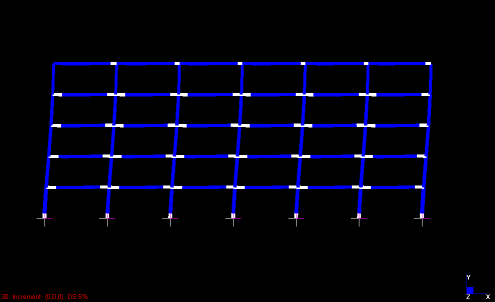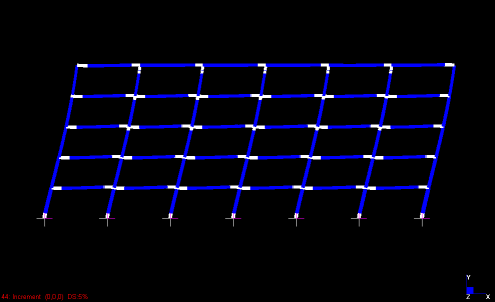
Fig. 4 Progressione della formazione di cerniere plastiche

 

Uniforme
 

Modale
 

softening
 

Rif. A
 

Rif. B
 

Rif. C
 

 

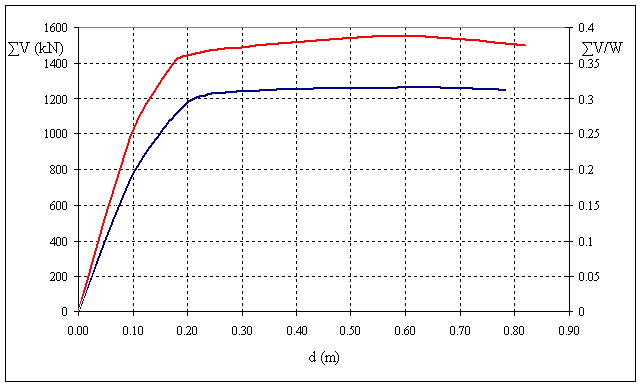
Fig. 5 Diagramma prodotto dal post-processore Straus7

 

La fig. 5 rappresenta una curva crescente fino ad un massimo oltre il quale si ha comportamento “softening”, dovuto ad effetti del secondo ordine. Per ottenere tale punto notevole conviene eseguire l’analisi statica non lineare in termini di spostamenti impressi piuttosto che forze impresse.

Sulla base di tale curva si ricava la curva equivalente di un sistema elasto-plastico ad un grado di libertà, introdotto per determinare la richiesta di spostamento della struttura soggetta all’azione sismica[1][2].

E’ possibile incrementando il carico orizzontale avere la progressione della formazione di cerniere plastiche fino a collasso e quindi la loro localizzazione nella struttura come rappresentato in fig. 6.

 

 

 

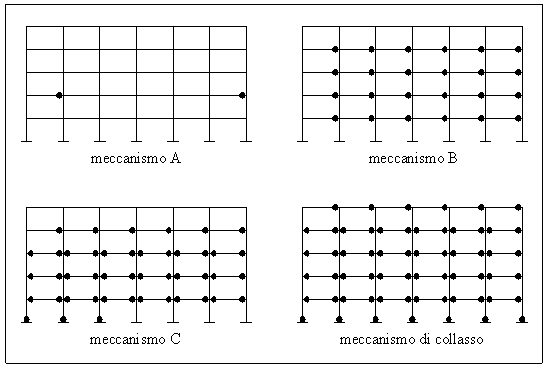
Fig. 6 Configurazione cerniere plastiche distribuzione uniforme

 

Inoltre si può valutare il comportamento isteretico di un un elemento beam, espresso mediante il diagramma momento curvatura, in cui è possibile vedere quanto l’elemento si sia plasticizzato e dedurre la sua duttilità.

 

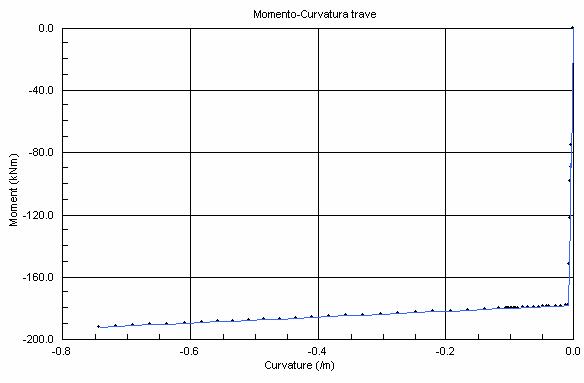
Fig. 7 Diagramma Momento-Curvatura di un elemento trave

 

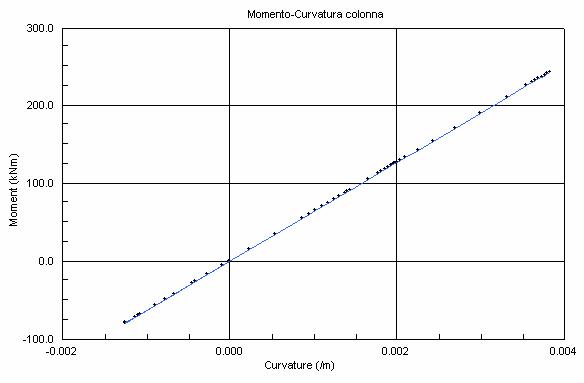
Fig. 8 Diagramma Momento-Curvatura di un elemento colonna

 

Analisi dinamica non lineare

 

Per tale analisi si devono introdurre degli accelerogrammi spettrocompatibili allo spettro di progetto elastico. Per questo motivo si è creato un programma di generazione di segnali sismici in C++[5].

 

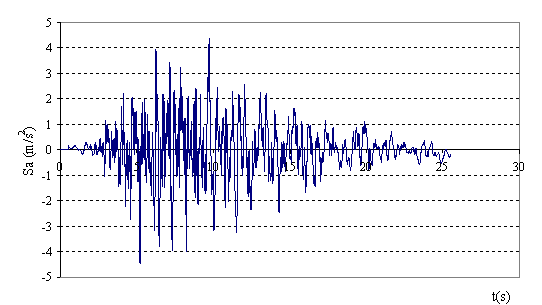
Fig. 9 Accelerogramma generato

 

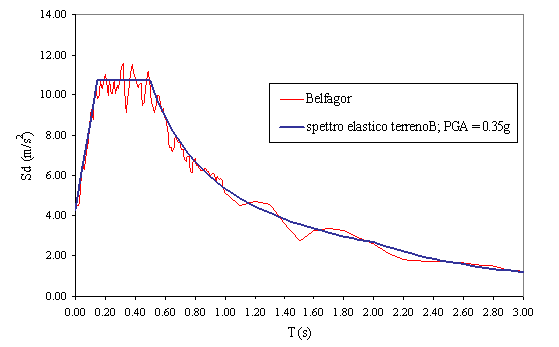
Fig. 10 Spettro di risposta

 

La norma consente anche l’uso di accelerogrammi registrati; sono stati usati quelli di El Centro, Tabas e Tolmezzo scalati all’accelerazione di progetto 0.35g.

I risultati espressi in termini di spostamento in sommità, da confrontare con il valore ottenuto dall’analisi statica non lineare, sono rappresentati nelle figure seguenti.

 

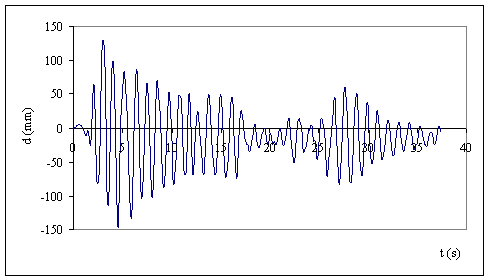
Fig. 11 Spostamento in sommità per l’accelerogramma di El Centro

 

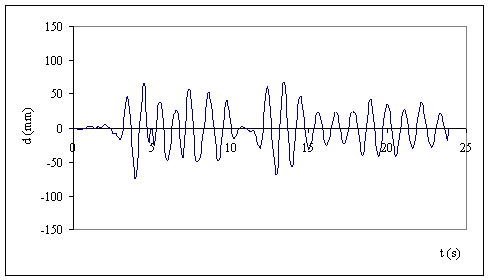
Fig. 12 Spostamento in sommità per l’accelerogramma di Tabas

 

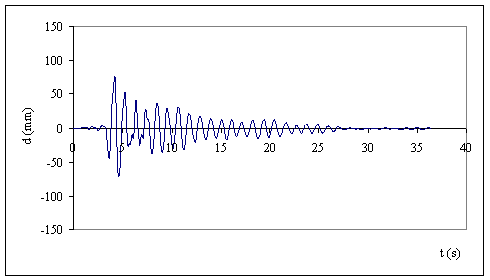
Fig. 13 Spostamento in sommità per l’accelerogramma di Tolmezzo

 

Dai grafici possiamo dedurre che l’equivalenza in termini di picco massimo PGA non è sufficiente per confrontare accelerogrammi registrati, è necessario tenere conto anche del contenuto in frequenza dell’accelerogramma per valutare i segnali sismici più gravosi in corrispondenza della frequenza del sistema che coinvolge più massa.

 

 

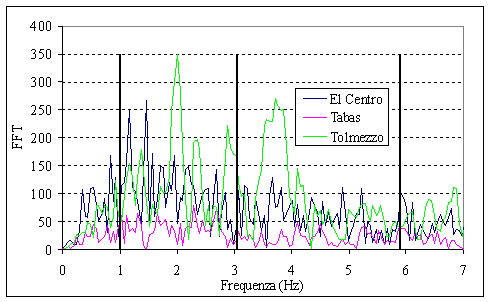
Fig. 14 Contenuto in frequenza

 

Anche in questa analisi è possibile valutare la configurazione di cerniere plastiche ed il comportamento isteretico degli elementi beam per risalire ad un valore indicativo di duttilità.

 

 

Fig. 15 Configurazione delle cerniere plastiche a collasso

 

 

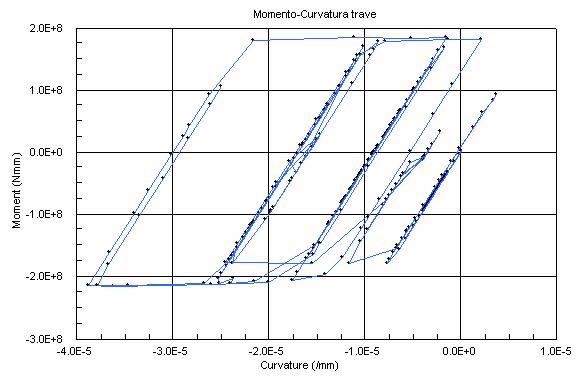
Fig. 16 Diagramma Momento-Curvatura di un elemento trave

 

 

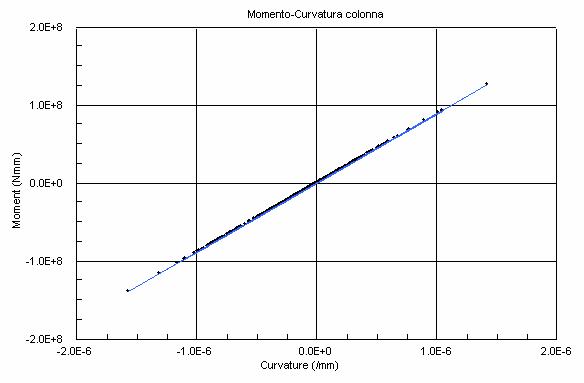
Fig. 17 Diagramma Momento-Curvatura di un elemento colonna

 

Conclusioni

 

Mediante il programma Straus7 è possibile, per i metodi di analisi proposti dall’Ordinanza, ottenere i seguenti risultati:

Questo consente di valutare le capacità di resistenza e di duttilità di strutture progettate con differenti metodi di progetto atti a sviluppare meccanismi di tipo globale.

Si possono così evitare meccanismi poco dissipativi o meccanismi che non proteggono gli elementi il cui cedimento strutturale è critico nei confronti della struttura; è infatti consigliabile la formazione di cerniere in tutte le sezioni di estremità delle travi piuttosto che delle colonne (fig.7,8,16,17).

 

Bibliografia

 

[1]        ORDINANZA PRESIDENZA DEL CONSIGLIO DEI MINISTRI n. 3274/20.03.03, "Primi elementi in materia di criteri generali per la classificazione sismica del territorio nazionale e di normative tecniche per le costruzioni in zona sismica"

[2]      UNI ENV 1998-1-1,2,3 EUROCODICE 8, “Indicazioni progettuali per la resistenza sismica delle strutture”

[3]        Ballio G.  Mazzolani F.M. (2002), Strutture in acciaio, Milano, Hoepli

[4]        Massonet C,.Save M. (1993), “Calcolo plastico a rottura delle costruzioni”, Milano, CittaStudi

[5]        Muscolino G. (2002), Dinamica delle strutture, Milano, McGraw-Hill