Università degli Studi di Padova – Facoltà di Ingegneria
DIPARTIMENTO DI INGEGNERIA MECCANICA
Tesi di Laurea Specialistica in Ingegneria Meccanica
ANALISI SPERIMENTALE E NUMERICA DELLA RESISTENZA
DI COLLEGAMENTI MONTANTE-TRAVERSO PER FACCIATE CONTINUE
CON UN MODELLO DI CALCOLO AGLI ELEMENTI FINITI
Relatori: PROF. BRUNO ATZORI (1)
ING. GIOVANNI MENEGHETTI (1)
CORRELATORE: ING. GIAMPIERO MANARA (2)
Laureando: LUCA FAVARIN
(1) Dip. di Ingegneria Meccanica, Facoltà di Ingegneria, Università di Padova
(2) R&E Department, Permasteelisa S.p.A., Vittorio Veneto (TV)
ABSTRACT
Le facciate continue a pannelli sono realizzate con delle serie di cellule costituite da una struttura in alluminio alla quale viene fissato il pannello cieco o vetrato (fig.1).
Tale struttura di alluminio è composta da elementi verticali, i montanti, ed orizzontali, i traversi, che sono bloccati tra loro tramite alcune viti in acciaio inox (fig.2). Il collegamento avviene attraverso viti autofilettanti in cave aperte.
|
Le facciate continue a pannelli sono realizzate con delle serie di cellule costituite da una struttura in alluminio alla quale viene fissato il pannello cieco o vetrato (fig.1).
Tale struttura di alluminio è composta da elementi verticali, i montanti, ed orizzontali, i traversi, che sono bloccati tra loro tramite alcune viti in acciaio inox (fig.2). Il collegamento avviene attraverso viti autofilettanti in cave aperte.
|

Fig. 1 - Pannello per facciata continua
Fig. 2 - Collegamento tra montante e traverso
Quando il pannello viene sollecitato dalla spinta del vento, e il carico trasferito ai traversi, tali collegamenti filettati risultano sollecitati, in quanto soltanto il montante è vincolato alle strutture primarie.
Dopo aver eseguito una serie di test di resistenza in laboratorio di tali accoppiamenti, volendo espanderne la valenza anche ad altri casi non testati, si è cercato di riprodurre, tramite il codice di calcolo agli elementi finiti Straus7, il comportamento delle giunzioni stesse, in modo da semplificarne lo studio e ridurre il numero di prove sperimentali future.
L’analisi quindi ha richiesto l’utilizzo di elementi di contatto, detti Point Contact, in modo da simulare il reciproco effetto di vite e cava.
Inizialmente si è eseguita un’analisi lineare elastica su un caso di contatto noto in letteratura, come primo approccio allo studio del problema del contatto.
Si è studiato quindi il contatto bidimensionale tra cilindro e semipiano (fig. 3), seguendo la teoria Hertziana e andando a cercare l’andamento delle tensioni lungo l’interfaccia tra i corpi a contatto.
|
Quando il pannello viene sollecitato dalla spinta del vento, e il carico trasferito ai traversi, tali collegamenti filettati risultano sollecitati, in quanto soltanto il montante è vincolato alle strutture primarie.
Dopo aver eseguito una serie di test di resistenza in laboratorio di tali accoppiamenti, volendo espanderne la valenza anche ad altri casi non testati, si è cercato di riprodurre, tramite il codice di calcolo agli elementi finiti Straus7, il comportamento delle giunzioni stesse, in modo da semplificarne lo studio e ridurre il numero di prove sperimentali future.
L’analisi quindi ha richiesto l’utilizzo di elementi di contatto, detti Point Contact, in modo da simulare il reciproco effetto di vite e cava.
Inizialmente si è eseguita un’analisi lineare elastica su un caso di contatto noto in letteratura, come primo approccio allo studio del problema del contatto.
Si è studiato quindi il contatto bidimensionale tra cilindro e semipiano (fig. 3), seguendo la teoria Hertziana e andando a cercare l’andamento delle tensioni lungo l’interfaccia tra i corpi a contatto.
|

Fig. 3 - Cilindro su semipiano
La modellazione è avvenuta sfruttando la simmetria e posizionando gli elementi di contatto nell’interfaccia tra i due corpi (figg. 4 e 5).
|
La modellazione è avvenuta sfruttando la simmetria e posizionando gli elementi di contatto nell’interfaccia tra i due corpi (figg. 4 e 5).
|
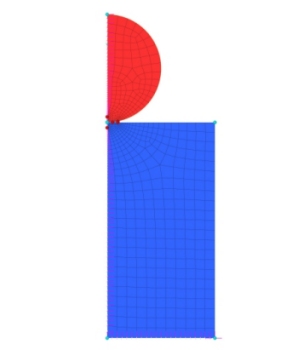

Fig. 4 - Cilindro su semipiano modellato Fig. 5 - Particolare della zona di contatto


Fig. 4 - Cilindro su semipiano modellato Fig. 5 - Particolare della zona di contatto
Si vuole allora cercare l’andamento delle tensioni normali sulle superfici dei corpi a contatto, a partire dal centro verso la periferia. Nella figura 6 è rappresentato il plottaggio di tali tensioni intorno alla zona del contatto, mentre in fig. 7 è riportato il confronto tra i risultati ottenuti con Straus7, sulle superfici di cilindro e blocco, e la soluzione analitica.
|
Si vuole allora cercare l’andamento delle tensioni normali sulle superfici dei corpi a contatto, a partire dal centro verso la periferia. Nella figura 6 è rappresentato il plottaggio di tali tensioni intorno alla zona del contatto, mentre in fig. 7 è riportato il confronto tra i risultati ottenuti con Straus7, sulle superfici di cilindro e blocco, e la soluzione analitica.
|
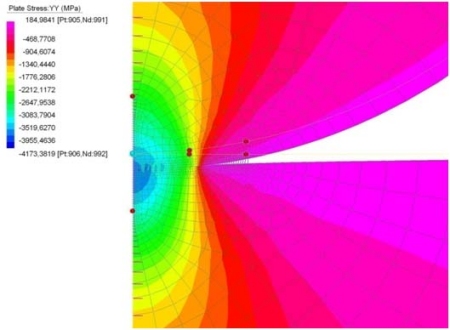
Fig. 6 - Tensioni normali alle superfici
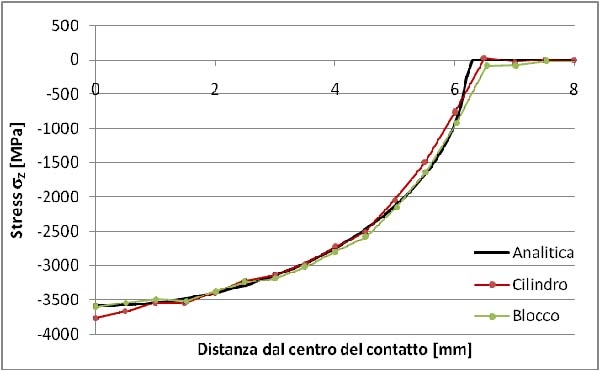
Fig. 7 - Confronto tra risultati analitici e numerici
Come si vede, il programma permette di riprodurre fedelmente i risultati analitici.
Successivamente si è iniziato con una simulazione del contatto tra la vite, sollecitata in una direzione, e la sua cava, così da riprodurre le analisi sperimentali effettuate in precedenza.
Si è proceduto per gradi, analizzando inizialmente il singolo accoppiamento tra una vite e la sua cava, modellati in due dimensioni, tenendo conto della non-linearità del materiale elasto-plastico.
Si sono confrontate le tensioni di von Mises sulla configurazione deformata con il comportamento reale delle cave a rottura, ottenendo il risultato illustrato dalle figure 8 e 9.
|
Come si vede, il programma permette di riprodurre fedelmente i risultati analitici.
Successivamente si è iniziato con una simulazione del contatto tra la vite, sollecitata in una direzione, e la sua cava, così da riprodurre le analisi sperimentali effettuate in precedenza.
Si è proceduto per gradi, analizzando inizialmente il singolo accoppiamento tra una vite e la sua cava, modellati in due dimensioni, tenendo conto della non-linearità del materiale elasto-plastico.
Si sono confrontate le tensioni di von Mises sulla configurazione deformata con il comportamento reale delle cave a rottura, ottenendo il risultato illustrato dalle figure 8 e 9.
|
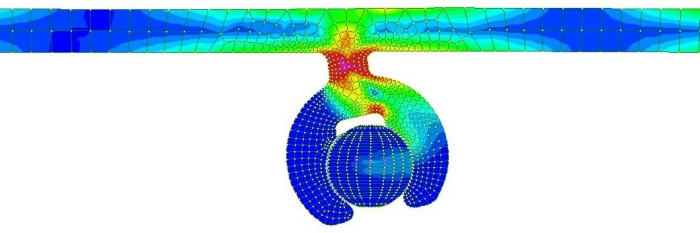
Fig. 8 - Risultati numerici 2D

Fig. 9 - Risultati sperimentali
Si osserva la corrispondenza tra le modalità di rottura delle analisi numeriche e di quelle sperimentali.
Successivamente si sono eseguite delle analisi in 3D, sempre con gli elementi di contatto Point Contact posizionati tra la vite e la cava (fig.10) e non-linearità materiale.
Anche per queste si è confrontata la configurazione deformata (fig. 11) con i risultati sperimentali.
|
Si osserva la corrispondenza tra le modalità di rottura delle analisi numeriche e di quelle sperimentali.
Successivamente si sono eseguite delle analisi in 3D, sempre con gli elementi di contatto Point Contact posizionati tra la vite e la cava (fig.10) e non-linearità materiale.
Anche per queste si è confrontata la configurazione deformata (fig. 11) con i risultati sperimentali.
|
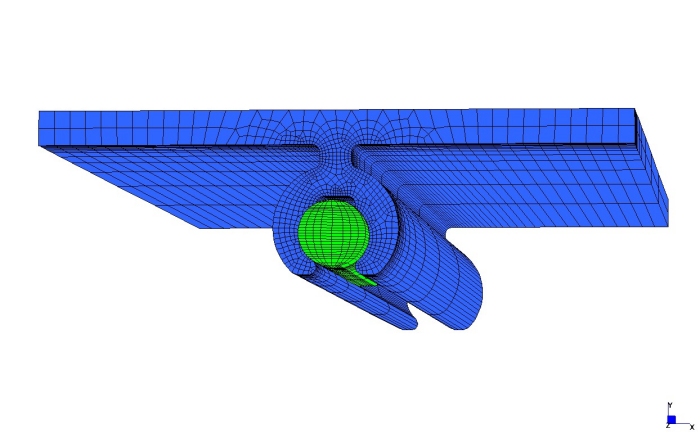
Fig. 10 - Risultati numerici 2D
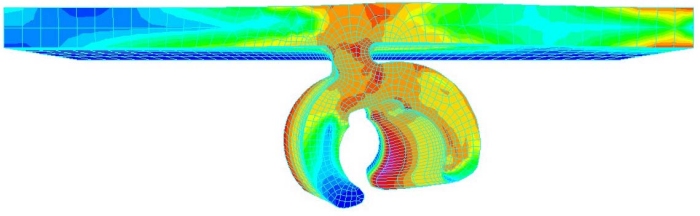
Fig. 11 - Risultati sperimentali
Per una ulteriore comparazione tra analisi numerica e sperimentale si sono sovrapposte le curve forza-spostamento ottenute da tale analisi agli elementi finiti e quelle ottenute dalle prove in laboratorio (fig.12).
|
Per una ulteriore comparazione tra analisi numerica e sperimentale si sono sovrapposte le curve forza-spostamento ottenute da tale analisi agli elementi finiti e quelle ottenute dalle prove in laboratorio (fig.12).
|
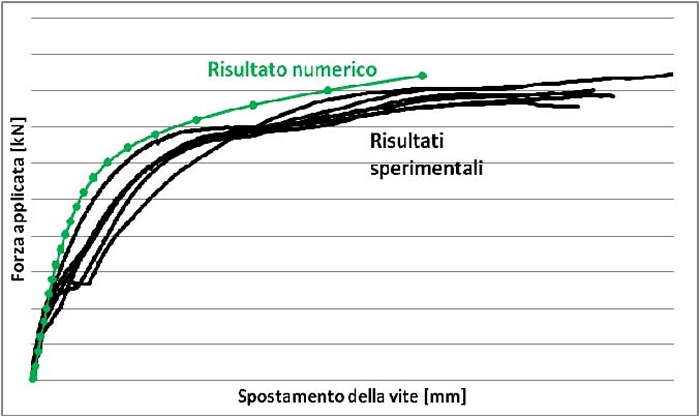
Fig. 12 - Curve forza-spostamento numerica e sperimentali
Come si osserva dal grafico si è ottenuta un’ottima corrispondenza tra le curve.
Come ultima serie di analisi si è modellato un giunto completo, utilizzando una combinazione di elementi Brick e Shell sfruttandone le simmetrie (fig. 13), in modo da diminuire il più possibile i tempi di calcolo.
|
Come si osserva dal grafico si è ottenuta un’ottima corrispondenza tra le curve.
Come ultima serie di analisi si è modellato un giunto completo, utilizzando una combinazione di elementi Brick e Shell sfruttandone le simmetrie (fig. 13), in modo da diminuire il più possibile i tempi di calcolo.
|
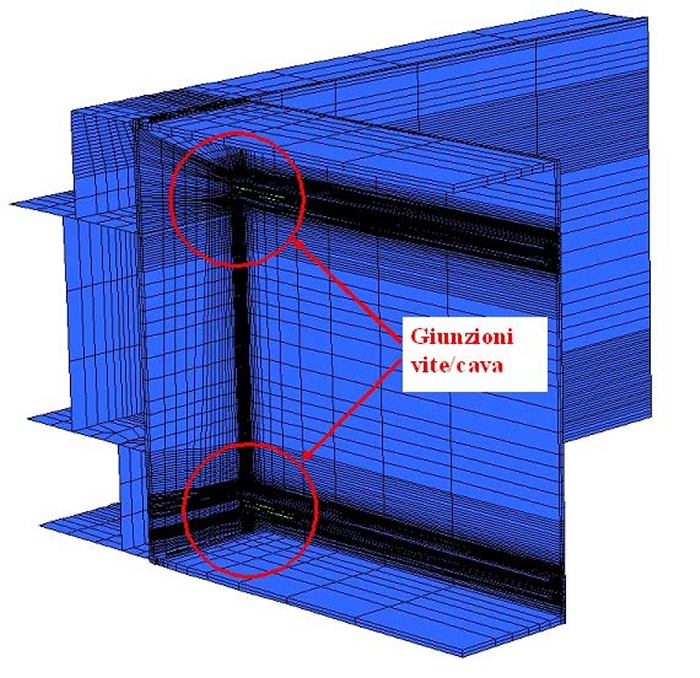
Fig. 13 - Modello del giunto
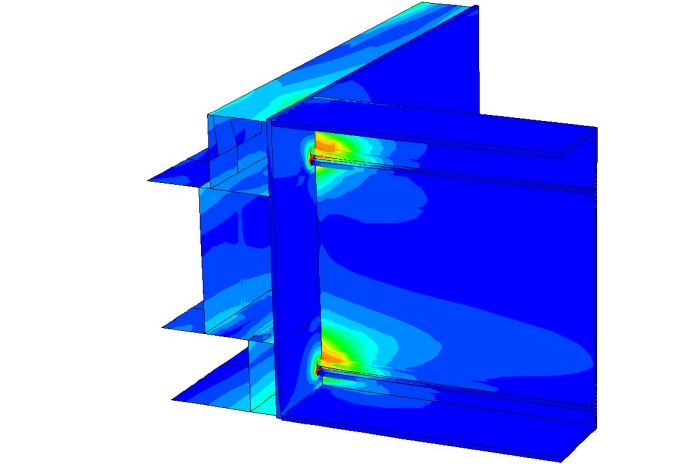
Fig. 14 - Tensioni di von Mises sul giunto deformato
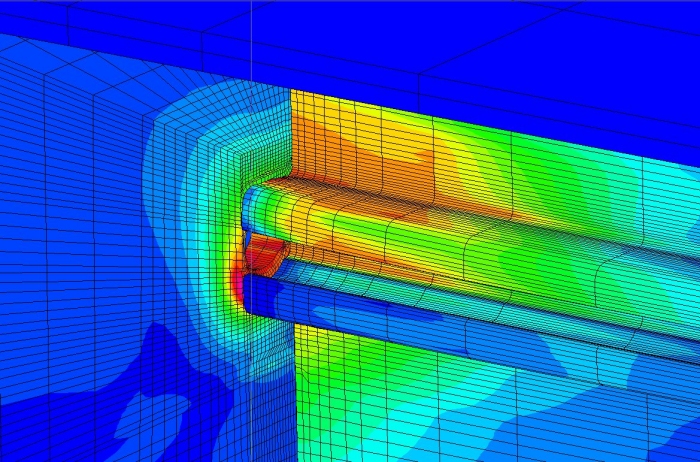
Fig. 15 - Particolare: cava superiore (vite nascosta)
Ancora una volta tali risultati, osservabili qualitativamente nelle figure 14 e 15, sono stati messi a confronto con i dati ottenuti dall’analisi sperimentale, mettendo in evidenza che globalmente le modalità di rottura corrispondono con quelle reali.
|
Ancora una volta tali risultati, osservabili qualitativamente nelle figure 14 e 15, sono stati messi a confronto con i dati ottenuti dall’analisi sperimentale, mettendo in evidenza che globalmente le modalità di rottura corrispondono con quelle reali.
|
Per inviare un messaggio: hsh@iperv.it