SOFTWARE PER L'INGEGNERIA


Via N. Tommaseo 13 - 35131 Padova tel. (049) 663888-8752724 Fax (049) 8758747


SAFEBALL
DOMINI DI RESISTENZA DI SEZIONI DI C.A. SOGGETTE A PRESSO-FLESSIONE DEVIATA


1 - CARATTERISTICHE GENERALI

Il programma di calcolo SAFEBALL costruisce i domini di resistenza dei parametri di sollecitazione relativi alla presso (tenso)-flessione deviata, di sezioni di c.a. di forma qualsiasi. Il programma è predisposto per operare sia nell'ambito del metodo delle Tensioni Ammissibili (T.A.) che in quello degli Stati Limite (S.L.). SAFEBALL è dotato di un'interfaccia grafica che rende facile e immediata l'introduzione della geometria della sezione e la visualizzazione dei risultati. SAFEBALL fornisce inoltre una relazione di calcolo riepilogativa.
SAFEBALL è disponibile per PC sotto sistema operativo MS-DOS.

2 - FONDAMENTI TEORICI E COMPUTAZIONALI

Si richiamano di seguito gli aspetti fondamentali dei due metodi di verifica, con riferimento alla normativa italiana (D.M. 14-02-1992) e alla tecnica computazionale utilizzata.

2.1 - Leggi costitutive dei materiali
Si stabiliscono le seguenti convenzioni:
·gli accorciamenti e le compressioni sono positivi (+);
·gli allungamenti e le trazioni sono negativi (-).
Essendo inteso che sono deformazioni unitarie, nel seguito si ometterà l'aggettivo unitario.
Le ipotesi di calcolo sulle quali si basa la verifica di resistenza di sezioni soggette a presso-flessione, comuni ad entrambi i metodi, sono le seguenti:
·le sezioni si conservano piane;
·assenza di scorrimento relativo fra calcestruzzo e acciaio,
·il calcestruzzo teso non dà contributo alla resistenza.
Metodo T.A.
Entrambi i materiali hanno comportamento elastico-lineare.
Calcestruzzo.
La tensione ammissibile viene definita mediante la formula:
dove indica la resistenza caratteristica cubica a 28 giorni.
Nelle solette di spessore minore di 5 cm. la tensione ammissibile è ridotta del 30%.
Nelle travi a T con soletta collaborante la tensione ammissibile è ridotta del:
·30% per soletta di spessore < 5 cm;
·10% per soletta di spessore> 5 cm.
Per pilastri calcolati a compressione semplice la tensione ammissibile assume il valore ridotto:
equazione
con s dimensione trasversale minima della sezione.
Nella sollecitazione di presso-flessione la tensione media dell'intera sezione non deve superare la tensione ammissibile . Quest'ultima prescrizione, porta ad escludere, come significativa, la parte del dominio resistente della sezione caratterizzata da uno sforzo normale , dove con si è indicata l'area ideale della sezione. Acciaio.
La tensione ammissibile non deve superare i valori riportati nella seguente tabella:
TIPO DI ACCIAIO (N/mmq)

...............Fe B 22 k 115
...............Fe B 32 k 155
...............Fe B 38 k 215
...............Fe B 44 k 255

Metodo S.L.

Calcestruzzo.

Per il calcestruzzo si assume la legge costitutiva parabola-rettangolo:
Fig. 1 - Legge costitutiva convenzionale di calcolo del calcestruzzo.
I parametri che definiscono tale legge sono:
· : resistenza caratteristica cilindrica;
· : resistenza di calcolo cilindrica;
In ogni caso lo sforzo normale N deve risultare minore di quello calcolato per la distribuzione costante di deformazione () con una maggiorazione del 25% del coefficiente . Questa prescrizione, porta ad escludere, come significativa, una parte del dominio resistente.
La deformazione limite è pari a 0.0035 nel caso di asse neutro intersecante la sezione, e variabile dal valore predetto a 0.0020 quando l'asse neutro, esterno alla sezione, tende all'infinito.

Acciaio.

Per l'acciaio si assume la legge costitutiva caratterizzata da un comportamento lineare elastico entro i limiti di snervamento e perfettamente plastico fino a rottura:
Fig. 2 - Legge costitutiva convenzionale di calcolo dell'acciaio.
I parametri che definiscono tale legge sono:
·: resistenza caratteristica di snervamento, funzione del tipo di acciaio come riportato nella seguente tabella:
TIPO DI ACCIAIO (N/mmq.)
................Fe B 22 k 215
................Fe B 32 k 315
................Fe B 38 k 375
................Fe B 44 k 430

· : resistenza di snervamento di calcolo;
· : coefficiente parziale di sicurezza;
· : modulo di elasticità longitudinale;
· : deformazione in corrispondenza dello snervamento di calcolo.

2.2 - Costruzione del dominio di resistenza.

Rispetto al sistema di riferimento baricentrico si stabiliscono le seguenti convenzioni: ·lo sforzo normale N è positivo se di compressione; ·il momento flettente Mx relativo all'asse x è positivo se tende le fibre della sezione che hanno coordinate; ·il momento flettente My relativo all'asse y è positivo se tende le fibre della sezione che hanno coordinate. Le equazioni generali di equilibrio della sezioni sono: equazione
dove:
è l'area lorda di calcestruzzo, , , , sono l'area, le coordinate e la tensione della i-esima armatura e m è il numero totale di posizioni di armatura.
Fissata una posizione dell'asse neutro, in conseguenza delle limitazioni convenzionalmente poste alle ( nel metodo T.A. (( nel metodo S.L.), è individuato un piano limite di tensione (deformazione); l'integrazione delle equazioni di equilibrio fornisce la terna di parametri di sollecitazione (N, Mx, My) che portano alla rottura convenzionale della sezione. L'insieme di tutte le terne forma una superfice chiusa che individua il dominio di resistenza tridimensionale della sezione soggetta a presso-flessione deviata.
Il metodo di integrazione utilizzato è il metodo delle strisce finite; esso sfrutta la proprietà delle funzioni integrande di essere costanti lungo la direzione parallela all'asse neutro. In generale un numero di strisce pari a 100 è sufficiente per una buona definizione del dominio di resistenza.
Sezionando il dominio tridimensionale con i due piani caratterizzati rispettivamente da Mx = 0 e My = 0 si ottengono i domini di resistenza bidimensionali (campi) relativi ai due casi di presso-flesssione retta. Se la sezione di calcestruzzo, unitamente alla distribuzione delle armature, presenta un'asse di simmetria è possibile costruire direttamente il relativo campo di presso-flessione retta, in quanto la direzione dell'asse neutro è nota a priori e risulta perpendicolare all'asse di simmetria in esame. Se la condizione di simmetria non è rispettata, è necessario ricorrere alla costruzione del dominio tridimensionale.

2.3- Verifica di resistenza.

Il dominio di resistenza è uno strumento indispensabile per la verifica di resistenza della sezione, alle più svariate condizioni e "storie" di carico. In generale, la verifica è effettuata verificando che la sollecitazione esterna S appartenga al dominio. In questa sede, la misura della sicurezza è fondata sulla ricerca del valore ultimo della sollecitazione affine (cioè a rapporti uguali fra le componenti non nulle) a quella indotta dalle sollecitazioni esterne. In altre parole, il percorso lungo il quale il punto rappresentativo della sollecitazione si muove per raggiungere la frontiera del dominio resistente è la retta uscente dall'origine e passante per il punto stesso. Indicata con R la resistenza in corrispondenza dell'intersezione tra il dominio di resistenza e la suddetta retta, la misura della sicurezza è data dal rapporto R/S. La prescrizione prevista nel metodo S.L. (D.M. 14-02-1992, par. 4.2.1.2.), relativa alle incertezze sul punto di applicazione dei carichi (eccentricità aggiuntiva), non è automaticamente inserita nel programma ma, deve essere prevista dall'utente nella fase di introduzione dei parametri di sollecitazione.

3 - ESEMPI

Sono riportati di seguito, i domini di resistenza di cinque sezioni. Le prime tre sono tratte dalla bibliografia e hanno lo scopo di confrontare i risultati forniti da SAFEBALL con le soluzioni teoriche. Il confronto consiste nel verificare che la sollecitazione ultima, fornita dal testo di riferimento, giace proprio sulla frontiera del dominio di resistenza costruito da SAFEBALL. Le ultime due sezioni si riferiscono invece, ad una sezione trasversale di una trave a "L" e ad una sezione trasversale di una pila da ponte. Nel primo e quarto esempio si è operato nell'ambito del metodo T.A., nei rimanenti del metodo S.L. Gli esempi qui proposti, mettono in evidenza le notevoli potenzialità offerte da SAFEBALL, anche nella fase di visualizzazione dei risultati. La rappresentazione grafica del dominio di resistenza è indispensabile per la corretta valutazione della sicurezza.

ESEMPIO 1 (Santarella L., 1990, pag. 333, es. 9)

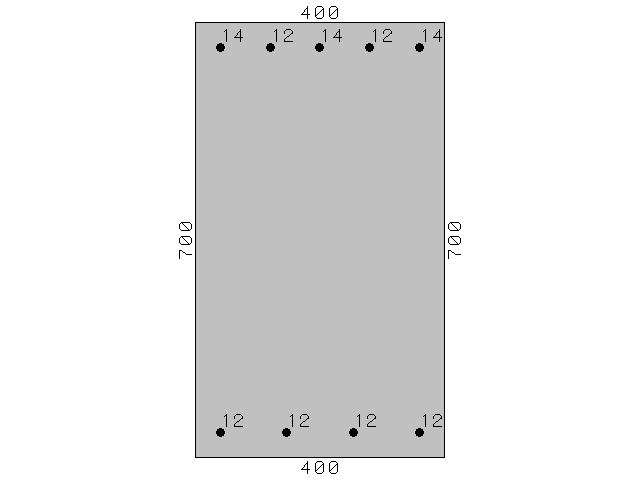Tensioni ammissibili: = 5 N/mmq = 120 N/mmq
Sollecitazione:
N = 200 kN
Mx = -100 kNm
My = 0 kNm
ESEMPIO 2 (Mola F., 1993, pag. 109)
Resistenze di calcolo: = 15.56 N/mmq = 347.83 N/mmq = 200000 N/mmq Sollecitazione:
N = 1493.8 kN ( = -0.4) Mx = 336.1 kNm (1 = 0.15) My = 149.4 kNm (2 = 0.10)
ESEMPIO 3 (Mola F., 1993, pag. 93) Resistenze di calcolo:
= 15.56 N/mm2 = 347.83 N/mm2 = 200000 N/mm2 Sollecitazione:
N = 2243.7 kN ( = -1.0) Mx = 538.5 kNm ( = 0.4) My = 0 kNm
ESEMPIO 4 Tensioni ammissibili: = 11 N/mmq = 255 N/mm2

ESEMPIO 5
Resistenze di calcolo: = 18.15 N/mmq = 373.91 N/mmq = 206000 N/mmq

RIFERIMENTI BIBLIOGRAFICI

C.E.B.: Manuel de Calcul "Flexion - Compression, (2e proposition de rédaction - Février 1972), Bull. d'information N° 82, Paris, Avril 1972.
C.E.B.: Manuel de Calcul "Flexion - Compression, (Final Draft - Avril 1980), Bull. d'information N° 135, Paris, Mai 1980.
D.M. 14-02-1992: Norme tecniche per l'esecuzione delle opere in cemento armato normale e precompresso e per le strutture metalliche, Suppl. ord. G.U., 18-03-1992, N° 65.
D.M. 09-01-1996: Norme tecniche per il calcolo, l'esecuzione ed il collaudo delle strutture in cemento armato, normale e precompresso e per le strutture metalliche, Suppl. ord. G.U., 05-02-1996, N° 29. Migliacci A. e Mola F.: Progetto agli stati limite delle strutture in c.a., Masson, 1990.
Mola F. (a cura di): Manuale C.E.B/F.I.P sulla flessione e forza normale, CittàStudi, 1993. Santarella L.: Il cemento armato - La tecnica e la statica, Hoepli, 1990.



HSH
STRAUS
STRAUS: scheda tecnica