SOFTWARE PER L'INGEGNERIA

Via N. Tommaseo 13 - 35131 Padova
tel. (049) 663888-8752724
Fax (049) 8758747
ESEMPI DI CALCOLAZIONI TIPO CODICE DI CALCOLO STRAUS
ANALISI TERMICHE NON LINEARI CON STRAUS

Sono state condotte una serie di analisi termiche su sezioni di calcestruzzo armato (pilastri, e solette) per valutare la diminuzione di resistenza della struttura dovuta all'esposizione ad un ipotetico incendio.
L'analisi effettuata ha richiesto l'individuazione:
- dell'incendio da applicare al modello. E' stato utilizzata la legge proposta nella UNI 9502 che riprende il DTU (Document Technique Unifiè 1974-1980):

T(t) = 20 + 345 log10( 8t+1 )


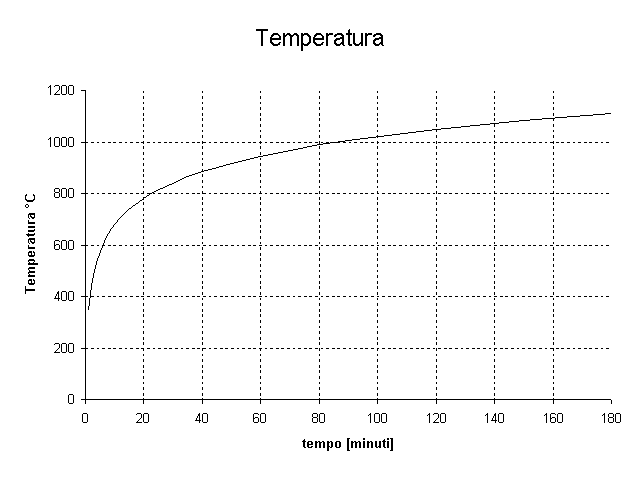
Figura 1 - Andamento della temperatura in funzione del tempo.


I parametri kX, kY, kZ r e c che definiscono l'equazione di diffusione del calore:

T=Temperatura
t=tempo
kX, kY, kZ=coefficienti di conduzione termica
ro=densità
c=calore specifico del materiale a pressione costante
Per i coefficienti di conduzione è stata assunta la legge di variazione in funzione della temperatura proposta nelle UNI 9502:
lambda = lambda(T) =1.63-1.74^(-3)T + 6.95 10^(-7) T^(2) (Wm-1 °C-1)

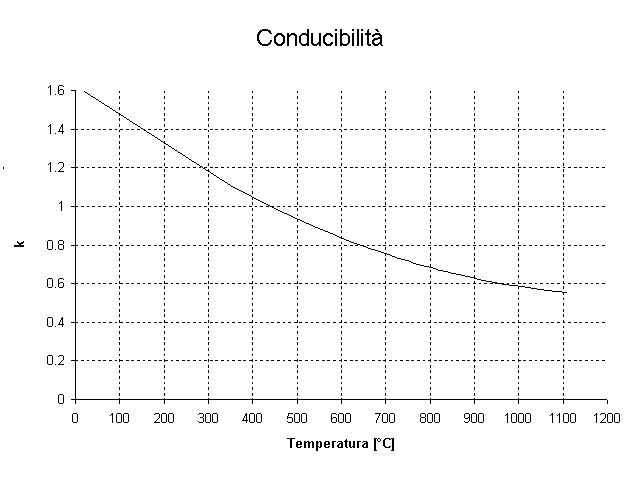
Figura 2 - Andamento della conducibilità in funzione della temperatura

Per la densità la relazione utilizzata è la seguente:
ro = ro(T) =2400 - 0.56 T (Kg m^(-3))

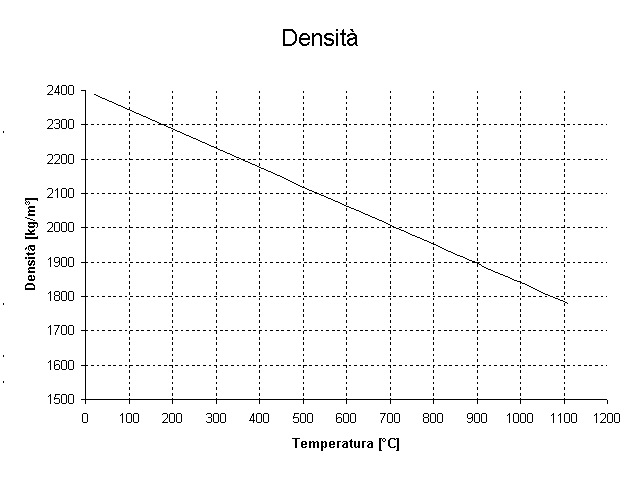
Figura 3 - Andamento della densità del calcestruzzo in funzione della temperatura
.

Parametri che definiscono le condizioni al contorno; in particolare:
-il coefficiente h relativo al trasferimento di calore per convezione:
qn=h (T-Ta)
-il coefficiente hr relativo al trasferimento di calore per radiazione:
q=hrsigmaA(T^4-Ta^4)
hr è il coefficiente di trasferimento termico per radiazione
sigma è la costante di Stefan Boltzman (5.67E-8 ( W/m^2K^4 )
A è l'area della superficie
Tè la temperatura del corpo
Ta è la temperatura ambiente.

Analisi con STRAUS.

La realizzazione di un analisi termica (non lineare) con STRAUS prevede il passaggio attraverso le seguenti fasi:
1-Creazione di una mesh ad elementi finiti. Può essere utilizzata la libreria di elementi finiti comprendente elementi mono, bi e tridimensionali (vedi scheda tecnica). La mesh può essere generata sia internamente a STRAUS (Figura 4) sia importata da modelli provenienti da altri software (NASTRAN, AUTOCAD, IGES).


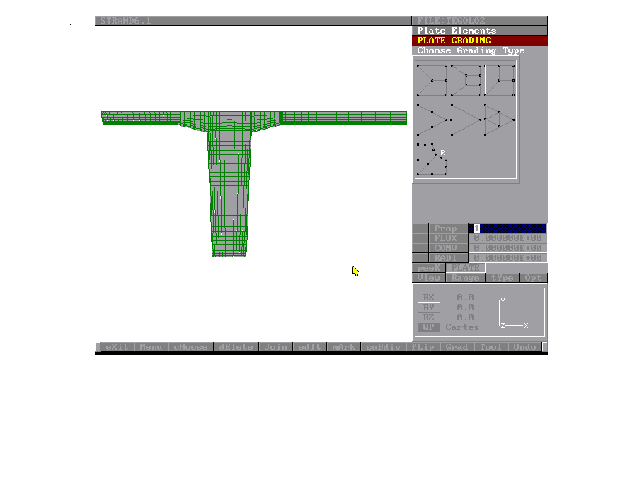
Figura 4 - Costruzione della mesh utilizzando elementi finiti LINEAR QUAD
.

2-Assegnazione delle proprietà dei materiali agli elementi in funzione:
-delle caratteristiche termiche dei vari materiali presenti (es. calcestruzzo, laterizio, ecc.)
-della temperatura ambiente, (vedi Figura 5).


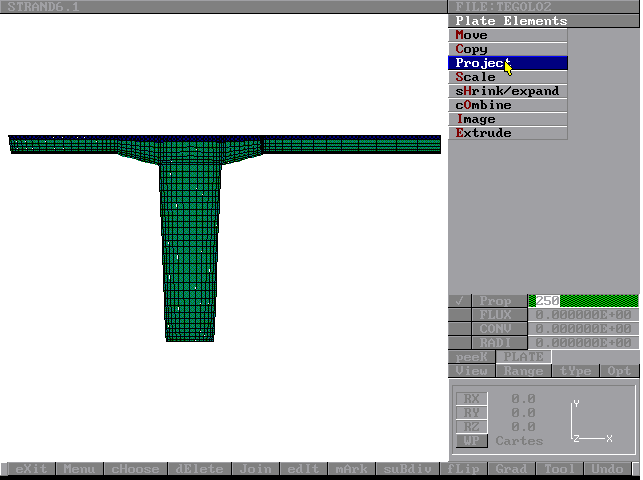
Figura 5 - Assegnazione delle proprietà agli elementi in funzione della temp. ambiente.


3-Assegnazione delle condizioni al contorno (Figura 6):
-temperature nodali
-gradiente termico
-trasferimento per convezione
-trasferimento per radiazione.

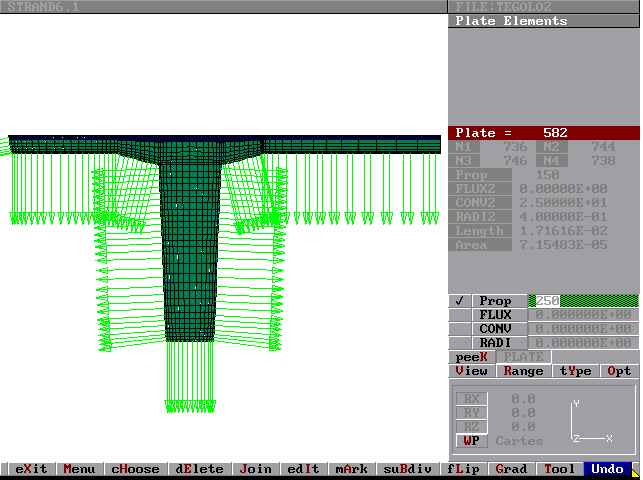
Figura 6 - Assegnazione delle condizioni al contorno.


4-Si definisce il set di proprietà nella sezione del programma dedicata all'introduzione delle caratteristiche termiche dei materiali (MENU - PROPERTY - MODO HEAT, Figura 7). In ciascun set può essere richiamata una "Temperature Table" (vedi fase successiva).

5-Definizione della "Temperature Table".
Nella sezione di STRAUS dedicata all'introduzione di tabelle si definiscono le leggi di variazione dei parametri:
-K(T), coeff. di conduzione
-Cp (T), calore specifico
-h(T), coeff. di convezione.
Nella Figura 8 sono proposte le leggi di variazione secondo le UNI 9502 per un calcestruzzo comune.

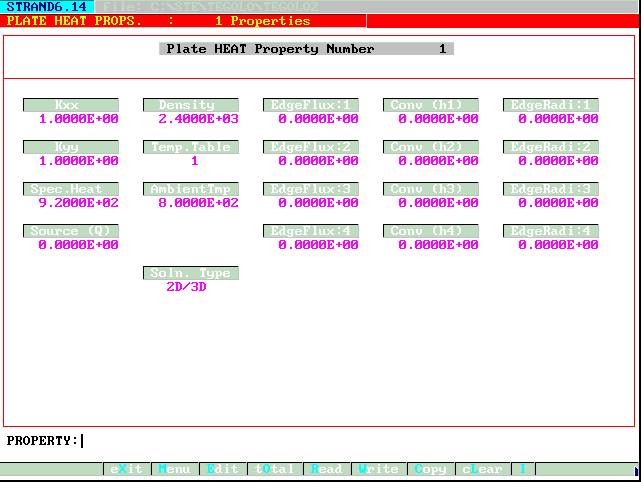
Figura 7 - Assegnazione del set di proprietà.


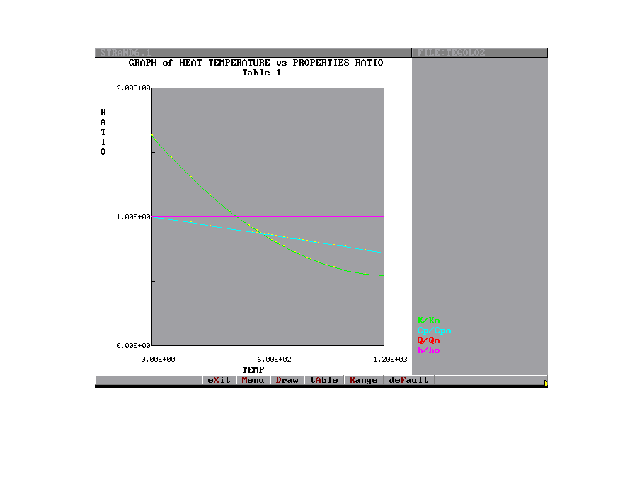
Figura 8 - Definizione della "Temperature Table"
.

6-Definizione dei parametri che governano la soluzione e della tabella dei tempi (compreso il numero di salvataggi, Figura 9 e Figura 10). Viene utilizzata una procedura File-Restart per poter aggiornare la temperatura ambiente (vedi Figura 7) in un certo numero di passi temporali.

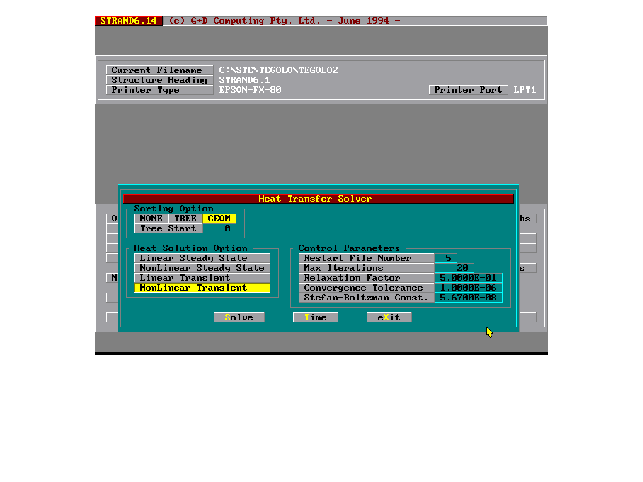
Figura 9: Parametri di HEAT SOLVER
.

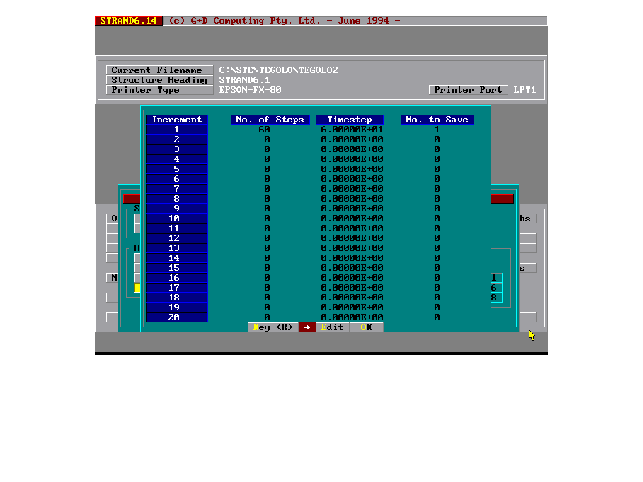
Figura 10:Definizione del time-stepping.


7-Lettura dei risultati.
STRAUS permette il post-processamento dei risultati in diverse forme (vedi scheda tecnica), in particolare:
-listati dei risultati, organizzati e selezionati a scelta dell'utente.
-diagrammi (eventualmente logaritmici) di grandezze relative a transitori (es. temperatura-tempo, Figura 11)
-contour cromatici o wireframe (Figura 12).
Le temperature trovate nell'analisi termica possono essere importate nel modo STRUCTURAL (analisi statiche, dinamiche, ecc.) ed essere quindi utilizzate come carico di tipo termico (temperatura imposta ai nodi). Per questo tipo di analisi STRAUS permette di assegnare il modulo elastico e il coefficiente di dilatazione termica variabili in funzione della temperatura.

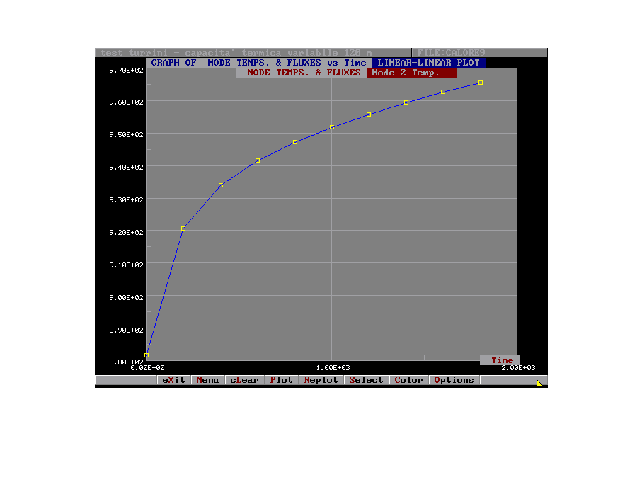
Figura 11:Andamento della temperatura in funzione del tempo
.

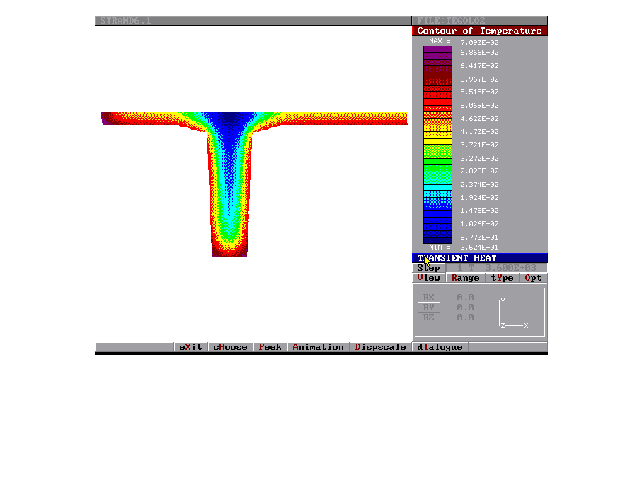
Figura 12:Contour della temperatura.


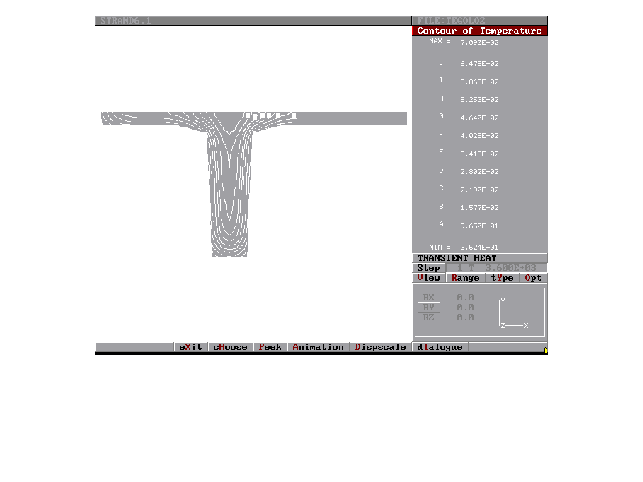
Figura 13:Curve iso-temperatura
.


HSH
STRAUS
STRAUS: scheda tecnica ______________________________________________
* Questo testo è stato prodotto utilizzando l'integrazione STRAUS-Microsoft Word 6.0, il binomio ideale per ottenere relazioni tecniche in forma tipografica (anche a colori). Le figure sono prodotte da STRAUS. Microsoft Word 6.0 consente di inserirle nel testo, aggiungendo commenti e modifiche. 6